目次 [非表示]
(前回の記事)
(続)カーツワイルのGNR論の「その後」を追う 〜 人工知能技術は、「塩基」という文字を用いて、生命の設計図を縦横無尽に記述・創作するゲノム工学の進化をどう後押ししているのか?
前回の記事の続きです。
カーツワイル氏が『ポスト・ヒューマン誕生』のなかで光を当てた3つの技術であるG: ゲノム工学・N:ナノ・テクノロジー・R:ロボティクス(+人工知能モデル)。
これらは、いずれも、記号配列が担う意味を解析し、編集するエンジニアリング技術であるのではないか?
本連載シリーズの初回の記事では、上記の問題提起を行いました、
第3回目となる今回の記事では、GNRのうち、N:ナノ・テクノロジーに光を取り上げます。
「記号配列が担う意味を解析し、編集するエンジニアリング技術である」ナノ・テクノロジーは、同じ情報解析・編集技術である深層ニューラル・ネットワークモデルを含む機械学習モデルや数理統計モデルの最新手法から、どのような影響を受けているのでしょうか?
これが、今回の記事の主題です。
取り上げるデータ解析手法
この記事では、ナノ・テクノロジーにおける情報解読・情報編集手法に影響を与えている機械学習モデルと数理統計モデルとして、以下の領域に焦点をあてます。
- TDA(Topological Data Analysis)モデル
- Deep Tensor Networkモデル
- GCN(Graph Convolutional Network)モデル
- (深層)強化学習モデル
- DNC(Differential Neural Computer) + GAN(Generative Adversarial Network)モデル
各手法が取るアプローチ:ナノテクノロジーとの親和性
情報解析のテクノロジーである数理モデルと機械学習の領域において、以下のような、物体のもつ「形状」(かたち)や、物体間に成立しうる(無数の観点で定義される無数の)関係や、物体間の相互影響関係を深掘りして解析することができる手法(アルゴリズム)が発見・開発されました。
情報解析テクノロジーがこのように発展したことで、物質の化学的な性質を原子・分子レベルで理解したり、人為的に編集・加工し合成することをミッションとするナノ・テクノロジーでできることが、増えてきています。
- TDA: 分子構造がもつ分子結合構造の「形状」(かたち)を数学上の厳密な言語で解析できる
- Tensor表現: 事物がもつ「無限種類」の「属性」間の関係を、テンソル分解の演算手法で可視化できる
- GCN:原子どうし、分子どうしの相互影響関係を表現した「グラフ構造」のデータを、深層ニューラル・ネットワークの枠組みで解析できる
- DNC+GAN:読み出し・上書き更新が可能な外部記憶メモリを用いた豊かなデータ解析能力・データ表現能力を用いたモデルで、物質がもつ原子・分子レベルの挙動・機能と属性を解析できる
ナノテクノロジー×AIの動向を論評した記事
上記の4つのデータ解析手法の発展が、ナノ・テクノロジー技術の進歩に対してどのような役割を果たしているのかを手法ごとに見ていく前に、ナノテクノロジー×AIの動向を論評した記事として、どのようなものがあるのかの事例を見てみましょう。
ナノテクノロジー×AIの動向を論評した記事としては、例えば以下があります。
上記の記事で言及されているドイツ議会の報告書は、以下になります。
ナノテクノロジー×AIの動向を取り上げている論考としては、冒頭の記事で取り上げられているものだけでも、次のものがあります。
- G M Sacha and P Varona(2013)Artificial intelligence in nanotechnology
- Anna Demming, EDITORIAL An intelligent approach to nanotechnology, Nanotechnology 24 (2013) 450201 (2pp)
- BOONSERM KAEWKAMNERDPONG, Programming Nanotechnology: Learning from Nature
- Novel Applications of Artificial Intelligence in Physical Sciences and Engineering Research (AIPSE) Academy Programme 2018–2021 aProgramme memorandum
- Itzik Malkielほか, Deep Learning for Design and Retrieval of Nano-photonic Structures
Kurtzweil.AIが注目している論文・論考
カーツワイル財団は、以下の論文に着目しているようです。
- FORESIGHT INSTITUTE, Machine learning may improve molecular design for nanotechnology
- Matthias Rupp et.al., Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning
東京大学ほかにおける機械学習の物質科学への適用事例
機械学習の物質科学への適用事例としては、例えば以下があります。
本記事は、AIモデル -> 物質科学・ナノテクノロジー の領域で最前線の論文を列挙的に眺めていく
この記事は、冒頭に述べた4つのデータ解析手法に光をあてて、情報解析モデルの発展が、物質科学とナノテクノロジーの領域の発展に対して、どのような影響を与えているのかを眺めていきます。
まずは、数学の位相幾何学の知見を用いたデータ解析手法である「パーシステントホモロジー」を駆使して、物質科学・ナノテクノロジーの課題に取り組んでいる取り組みを取り上げてみます。
「パーシステントホモロジー」については、以下が参考になります。
遺伝情報解析におけるAI技術(1)〜TDAモデル
事物がもつ「形状」(かたち)を数学の言語で厳密に解析する技法として、しばしば「柔らかい幾何学」とも形容される位相幾何学(Topology)があります。
この位相幾何学の解析ツールを活用して、物質をナノ・スケールで見たときに立ち現れてくる(物質がもつ)分子結合構造(の形状)がもつ特徴量を客観的・数学的に抽出した上で、その物質がどのような性質や機能・効能・薬効を持つのかを推定したり、類似した機能や効能・薬効をもつ物質を探索的に発見・分類する試みが行われています。
(代数的)位相幾何学が、形状(かたち)の類似性の観点から事物を分類するのに際して、「形状」(かたち)がもつ本質的な特徴として、着目する(よりどころとする)のは、数学の言葉で、位相的不変量とよばれています。
例えば、次のように定義されています。以下、引用文中の改行と太字は小野寺によるものです。
多様体のトポロジー研究では,多様体を位相的に区別するのに役立つような道具,すなわち位相不変量 (topological invariant) が重要である.
よく知られた位相不変量として,多様体 X 内の点 x を基点とする基本群(fundamental group)π1(X, x) やホモトピー群(homotopy group)πq(X, x),ホモロジー群 (homology group) H∗(X) やコホモロジー群 (cohomology group)H∗(X) がある.
トポロジーは、何らかの形(かたち。あるいは「空間」)を連続変形(伸ばしたり曲げたりすることはするが切ったり貼ったりはしないこと)しても保たれる性質(位相的性質(英語版)または位相不変量)に焦点を当てたものである[1]。
位相的性質において重要なものには、連結性およびコンパクト性などが挙げられる[2]。 位相幾何学は、空間、次元、変換といった概念の研究を通じて、幾何学および集合論から生じた分野である[3]。
(中略)
代数的位相幾何学
代数的位相幾何学は位相空間を調べるのに抽象代数学由来の道具を用いる数学の一分野である[8]。
その基本的な最終目的は同相を除いて位相空間を分類する代数的不変量を求めることであるが、普通はホモトピー同値を除いて大まかな分類を得ることが目的となる。
そのような不変量として最も重要なのがホモトピー群、ホモロジー群およびコホモロジー群である。
代数的位相幾何学では位相的問題を調べるのに代数学を用いることが主だけれども、位相を用いて代数的問題を解くということも時には可能である。例えば代数的位相幾何学で「自由群の任意の部分群がまた自由となること」を簡便に示すことができる。
今回取り上げるTDA(Topological Data Analysis)という手法は、「不変量」として、「ホモロジー」に注目します。
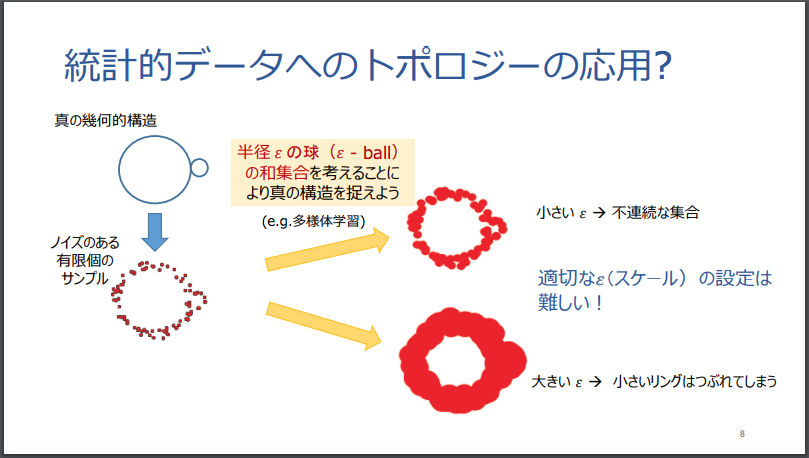
TDAでは、対象とする物体を観測(観察)する「ものさし」の大きさを、「尺が小さいものさし」から「尺が大きいものさし」へと連続的に変えていったときに、物体が持つ形状の本質的な特徴である「不変量」が、どのように変化していくのかを観測する「パーシステント・ホモロジー」と呼ばれる手法が、採用されています。
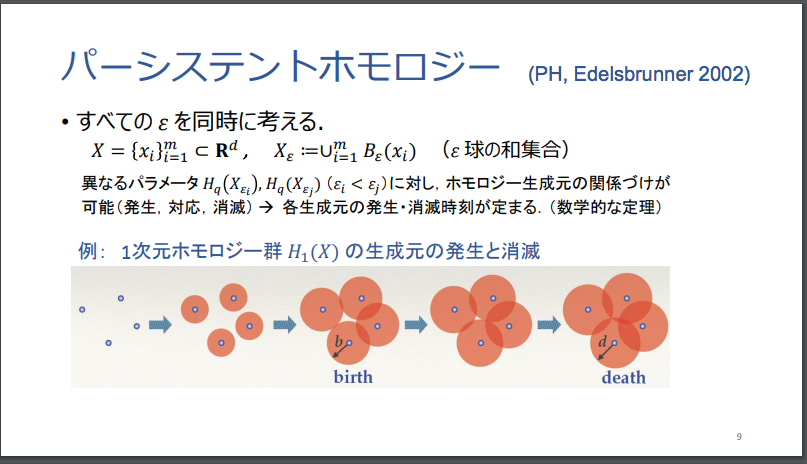
パーシステント・ホモロジーとは?
Wikipedia(英語版)では、以下の解説文があります。
Persistent homology is a method for computing topological features of a space at different spatial resolutions. More persistent features are detected over a wide range of spatial scales and are deemed more likely to represent true features of the underlying space rather than artifacts of sampling, noise, or particular choice of parameters.[1]
To find the persistent homology of a space, the space must first be represented as a simplicial complex. A distance function on the underlying space corresponds to a filtration of the simplicial complex, that is a nested sequence of increasing subsets.
対象とする物体を観測する「ものさし」の尺の大きさを連続的に変えていった場合に、形状の特徴量(「不変量」)である「穴」の数と位置が、連続的にどのように変化するのかを観測することで、対象物体がもつ立体的な形状の特徴の全体像を捉えます。
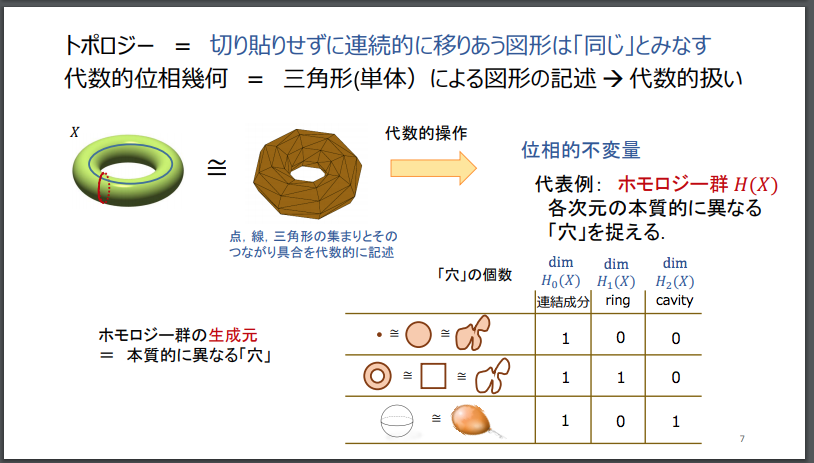
位相幾何学における「不変量」
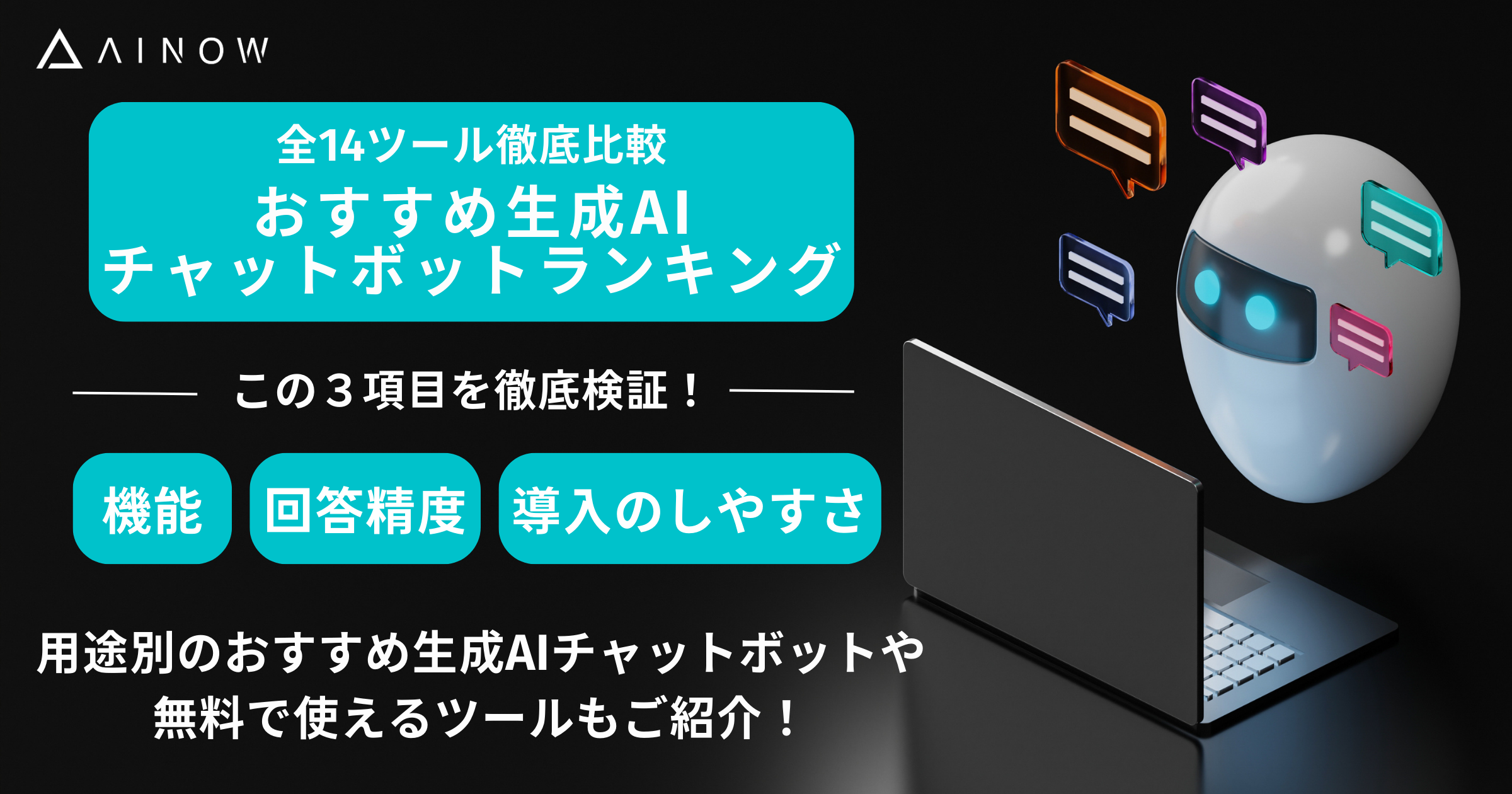
位相幾何学においては、それぞれの事物の形状がもつ本質的な特徴量(「不変量」)として、物質の形状に見られる「穴」の数と位置に注目します。
物質の形状に見られる「穴」の数と位置が、当該物体を観察するものさしのサイズ(スケールのサイズ)を少しずつ、連続的に変えてった場合に、どのように変化していくのか(穴が出現する「ものさしの大きさ」と、その穴が消滅する「ものさしの大きさ」に着目)を調べていくことで、対象物のかたち(形状)がもつ位相幾何学上の「本質的な特徴」を捉えていきます。
図形を「位相不変量」を用いて定量表現した例
鍛冶 静雄 「柔らかい幾何の拡がり -トポロジーの応用-」より転載。

鍛冶 静雄 「柔らかい幾何の拡がり -トポロジーの応用-」より転載。

鍛冶 静雄 「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
続けて、以下の福水氏のスライドを借用して見てみます。
福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
位相不変量の視覚表現(1):「パーシステント図」
上記のステップを経て、「パーシステント・ホモロジー」法は、アウトプットとして、以下のような縦横2次元(縦横2軸)のグラフが出力されます。
着目するスケールのサイズを連続的に変えていく過程で、物質の形状がもつ「穴」が発生する段階(スケールの大きさ)と消滅する段階(スケールの大きさ)が、2次元のグラフに出力されます。
この2次元グラフを複数の物質どうしで比較することで、それらの物質がもつ「かたち」が、位相幾何学の観点からみて、互いにどれだけ近しい距離にあるのか、という意味のある「情報」を抽出することができます。
以下、平岡 裕章 「位相的データ解析の基礎と応用」より、スライドを抜粋して転載致します。
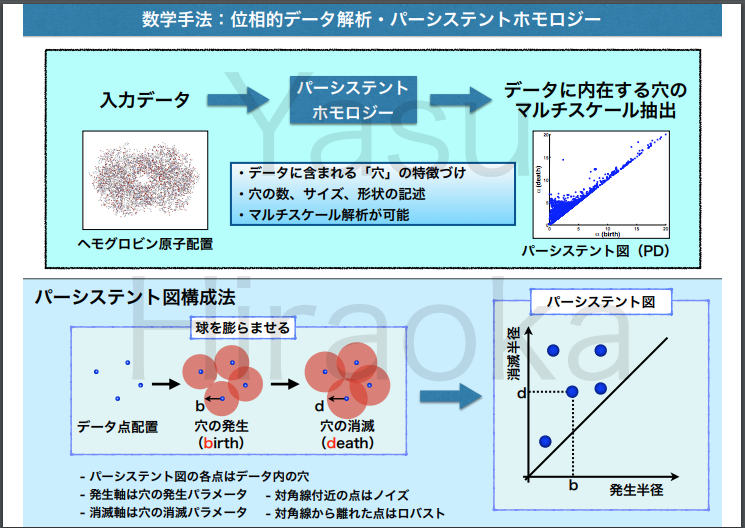
平岡 裕章 「位相的データ解析の基礎と応用」より転載。
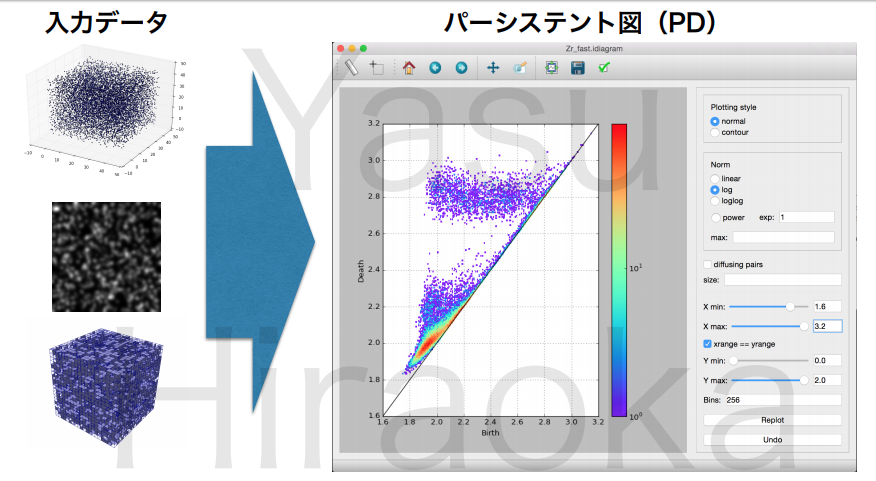
平岡 裕章 「位相的データ解析の基礎と応用」より転載。
位相不変量の視覚表現(2):「バーコード」
なお、先ほど引用した福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisの次のスライドによると、「パーシステント・ホモロジー」(PH)を視覚的に表現する可視化手法としては、ここまでみてきた「パーシステント図」のほかに、「バーコード」と呼ばれる表現方法があるようです。
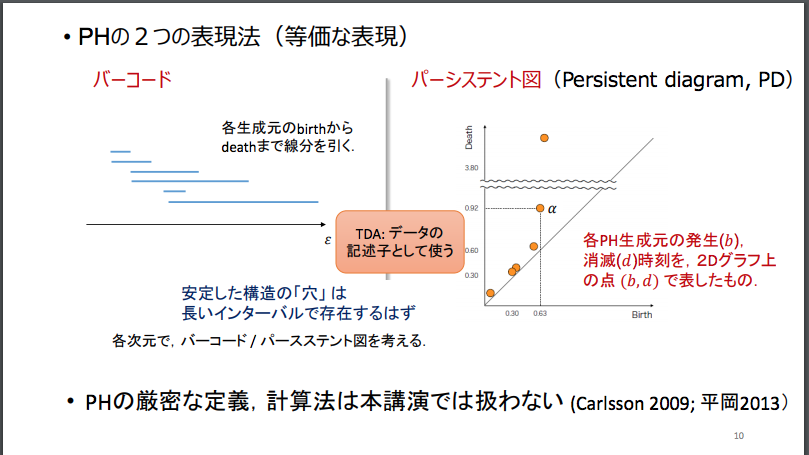
福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
この「バーコード」という表現手法を提案した論文は、以下になります。
この論文の冒頭に掲げられている概要(Abstract,)は、以下の文章になります。
Abstract.
This article surveys recent work of Carlsson and collaborators on applications of computational algebraic topology to problems of feature detection and shape recognition in high-dimensional data.
The primary mathematical tool considered is a homology theory for point-cloud data sets — persistent homology — and a novel representation of this algebraic characterization — barcodes. We sketch an application of these techniques to the classification of natural images.
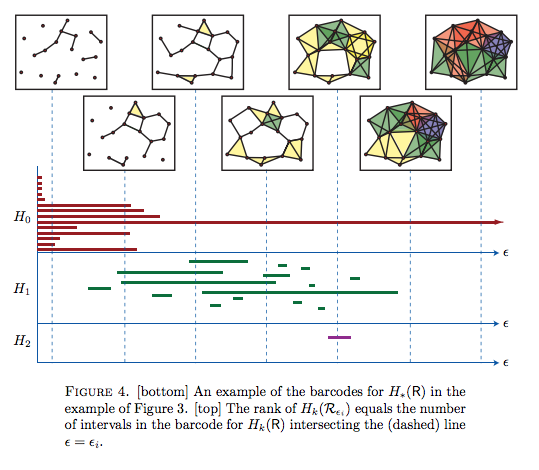
Robert Christ, BARCODES: The persistent topology of data論文よりFIGURE4を転載。
「パーシステント・ホモロジー」(PH)の可視化手法(表示方法)については、以下も参考になります。
パーシステント図による可視化事例:ある物質の「液相」(「液体」の状態)と「ガラス相」(「個体」の状態)の形状の違い
なお、福水氏のスライドでは、「パーシステント図」を用いて、ある物質(SiO2)が「液体」の状態(液相)と、「個体」の状態(ガラス相)とで、物質の形状の違いがどのように可視化されるかの事例が掲載されています。以下、その可視化の様子を転載します。
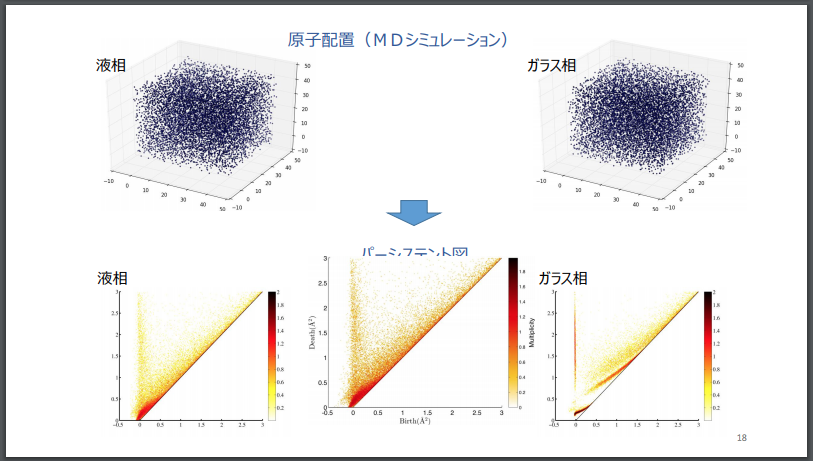
福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
このように、「パーシステント図」を用いることで、物質の形が持つ特徴(不変量)を視覚的に可視化することができます。
「パーシステント図」を定量的・数理的に解析する手法
この「パーシステント図」の視覚的な描像を人間が目で見ることで、ある物質の形状を解釈したり、複数の物質どうしの形の近さや遠さを比較することができます。
他方で、「パーシステント図」を人間の肉眼によって、主観的(感性的)に解釈するのではなく、「パーシステント図」を定量的な指標にデータ変換することで、客観的・数理的に取り扱う手法も開拓されています。
そのなかには、深層ニューラル・ネットワークモデルを用いた手法も提案されています。
以下の論考では、「カーネル法」を用いた手法が提案されています。
以下は、Wikipedia(日本語版)に掲載されている「カーネル法」の解説文です。
カーネル法(カーネルほう)はパターン認識において使われる手法の一つで、 判別などのアルゴリズムに組み合わせて利用するものである。よく知られているのは、サポートベクターマシンと組み合わせて利用する方法である。
パターン認識の目的は、一般に、 データの構造(例えばクラスタ、ランキング、主成分、相関、分類)を見つけだし、研究することにある。この目的を達成するために、 カーネル法ではデータを高次元の特徴空間上へ写像する。特徴空間の各座標はデータ要素の一つの特徴に対応し、特徴空間への写像(特徴写像)によりデータの集合はユークリッド空間中の点の集合に変換される。特徴空間におけるデータの構造の分析に際しては、様々な方法がカーネル法と組み合わせて用いられる。特徴写像としては多様な写像を使うことができ(一般に非線形写像が使われる)、それに対応してデータの多様な構造を見いだすことができる。
筆者の研究は, “(データの幾何形状を表現した)パーシステント図を見てその違い を判別する”という恣意的な作業を“パーシステント図に対する統計解析・機械学習1の 手法を確立して, その手法を用いて定量的に違いを評価する”に変える事である.
ここでは, パーシステント図に対する統計解析・機械学習手法としてカーネル法を用いる.
(中略)
筆者はパーシステント図に対するカーネル法として, 福水健次氏(統数研), 平岡裕章氏(東北大)との共同研究でPersistence weighted Gaussian kernel (PWGK, [KFH16, KFH17])を提 案して, 数理的性質の研究とデータ解析を行っている.
材料科学への応用では液体ガラ ス転移点問題を主成分分析や変化点検出により特徴付け, タンパク質の構造解析では サポートベクターマシンによる二値分類を行った. 本講演ではパーシステントホモロジー, パーシステント図のカーネル法の構成法, 数値計算結果を紹介する.
本稿の残りは, 以下のキーワードの解説に当てる.
1章 パーシステントホモロジー・パーシステント図.
2章 Persistence weighted Gaussian kernel
上記の論考で取り上げられている論文は、以下になります。
最初のKusano et.al (2016)の論文は、深層ニューラル・ネットワークの論文も数多く掲載されている情報科学領域で最高峰に位置づけられる国際論文誌(Tier 1 Conference, Top Conference)であるICMLに掲載されたもので、論文執筆人は3人とも日本人です。
- Genki Kusano, Kenji Fukumizu, and Yasuaki Hiraoka. Persistence weighted gaussian kernel for topological data analysis. In International Conference on Machine Learning, pages 2004–2013, 2016.
- Genki Kusano, Kenji Fukumizu, and Yasuaki Hiraoka. Kernel method for persistence diagrams via kernel embedding and weight factor. arXiv preprint arXiv:1706.03472, 2017.
- Afra Zomorodian and Gunnar Carlsson. Computing persistent homology. Discrete & Computational Geometry, 33(2):249–274, 2005.
以下は、人間の指紋(Fingerprints)を、特徴量(不変量)としての「パーシステント・ホモロジー」を頼りにデータ解析した事例です。
(サーベイ論文)パーシステント・ホモロジーを取り扱う機械学習モデルに係る技術動静
この論文は2018年11月にArxiv.リポジトリに公開されたもので、最近の潮流として、生データを入力値として受け付けてから、パーシステント・ホモロジー図(PH図)に変換し、さらにカーネル法を用いてPH図を高次元空間に写像した後に、機械学習の分類器や予測器に中間データを受け渡して、分類結果・予測結果を出力する、という一連の流れを紹介しています。
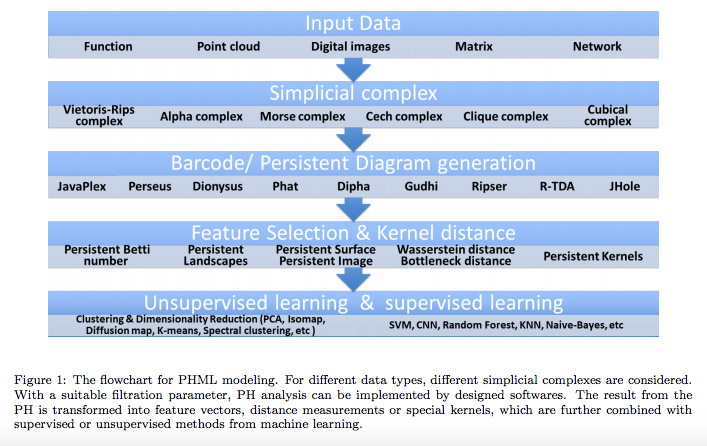
Chi Seng Pun et.al., Persistent Homology-based Machine Learning and its Applications – A Survey, Arxiv, 2018より転載。
この論文は、このような解析モデルが、どのようなソフトウェアを用いて、どのようなデータに対して適用されているのかも概説しています。
以下の図表には、対象となるデータの類型別に、頻繁に使われているソフトウェアと、PHの種類が掲載されています。
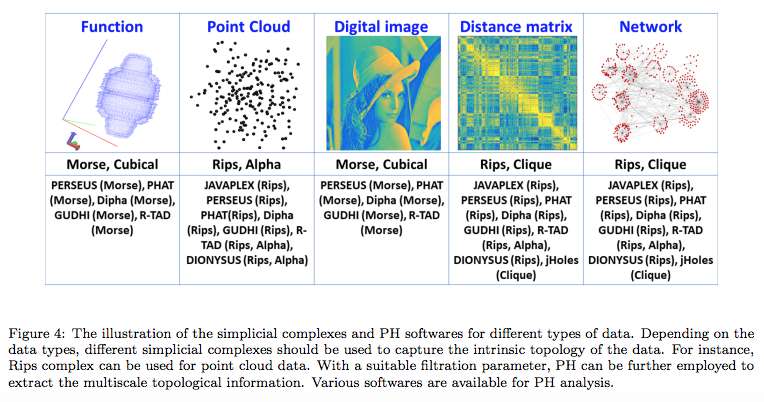
Chi Seng Pun et.al., Persistent Homology-based Machine Learning and its Applications – A Survey, Arxiv, 2018より転載。
以下は、タンパク質(Protein)の分子結合の構造図を、入力データとして受け取った場合の例です。
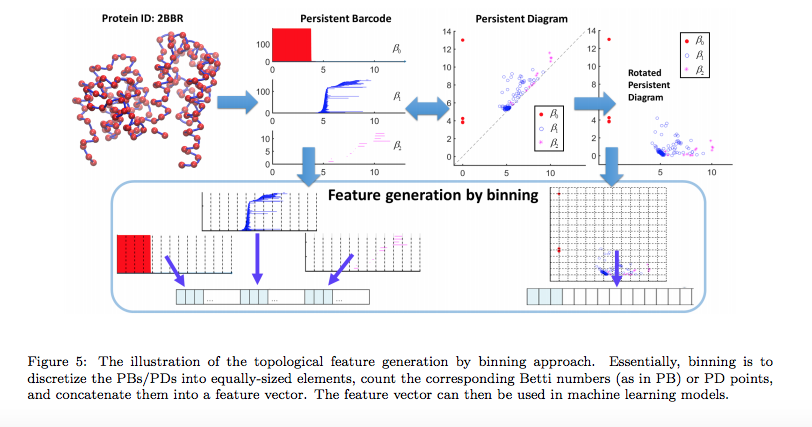
Chi Seng Pun et.al., Persistent Homology-based Machine Learning and its Applications – A Survey, Arxiv, 2018より転載。
「パーシステント図」を入力値として受け取る深層ニューラル・ネットワークモデルの例
「パーシステント図」を入力値として受け取る深層ニューラル・ネットワークモデルとしては、以下が提案されています。
この論文は、入力層で、これまでみてきた「パーシステント図」を受け取っています。
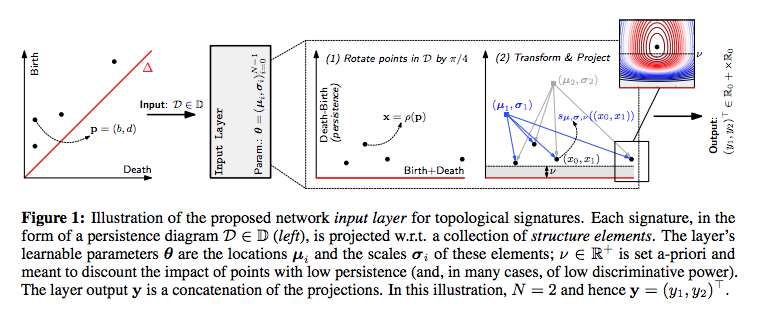
Christoph Hofer et.al., Deep Learning with Topological Signatures, Arxiv, 2018よりFigure 1を転載。
このモデルの精度検証(Experiments)としては、まず最初に、2次元の動物の画像をクラス分類するタスクに取り組んでいます。以下は、論文からの引用です。
“We apply persistent homology combined with our proposed input layer to two different datasets of binary 2D object shapes: (1) the Animal dataset, introduced in [3] which consists of 20 different animal classes, 100 samples each; (2) the MPEG-7 dataset which consists of 70 classes of different object/animal contours, 20 samples each (see [21] for more details).”
このタスクに取り組んだ結果は、以下になります。

同論文より、Figure 3を転載。
続けて2つ目のタスク(Experiment)として、ソーシャル・ネットワークデータ(グラフ形式のネットワーク・データ)の解析にも、同モデルを適用しています。論文に掲載されている結果は、以下になります。
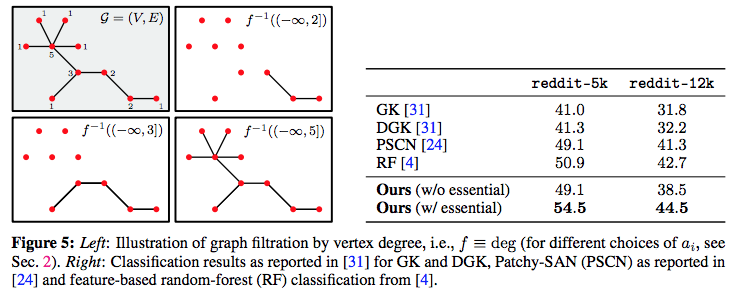
同論文よりFigure 5を転載。
生体分子(biomolecular)を含む分子構造データに対する適用例
次の論文は、生体分子を対象としたデータ解析に取り組んでいる事例です。
カーツワイル氏が『ポスト・ヒューマン誕生』で述べていたように、物質の原子・分子構造を解析するナノ・テクノロジーは、生命体のからだを構成する生体分子の機能や挙動の仕組みを解析することにも用いられます。
この領域は、同氏の唱えるGNR論のうち、「G」遺伝学と「N」ナノ・テクノロジーとが交差する領域です。
次の論文は、そのような「G」と「N」との交差領域で、位相幾何学の知見(「パーシステント・ホモロジー」特徴量・不変量の算出技術)を用いて、深層ニューラル・ネットワークモデル(畳み込みニューラル・ネットワークモデル)を適用している事例に該当します。
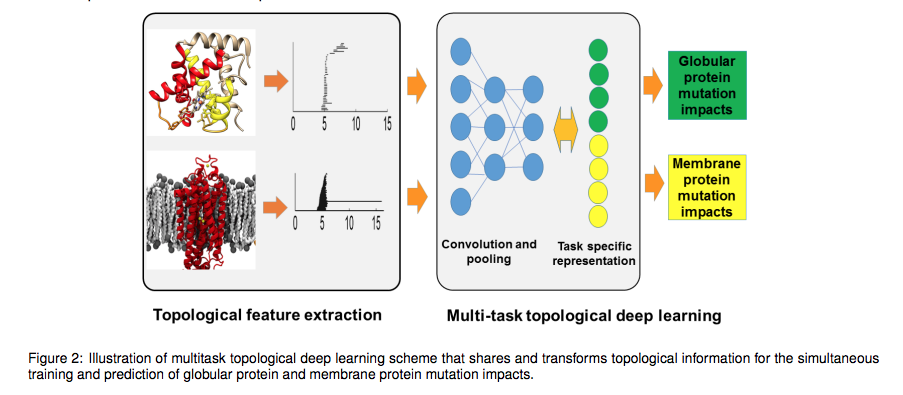
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
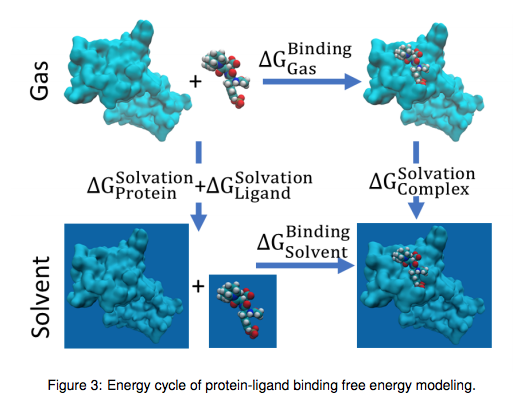
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
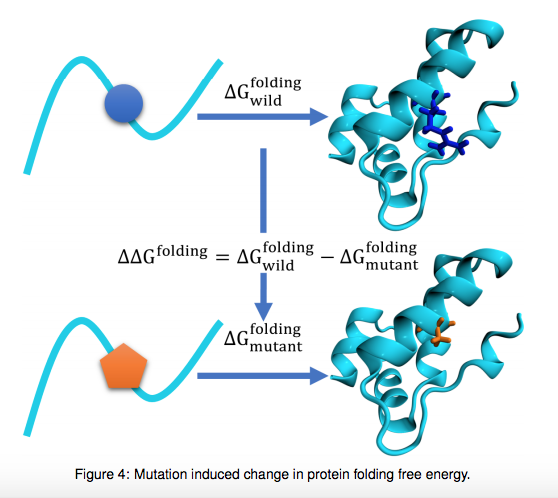
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
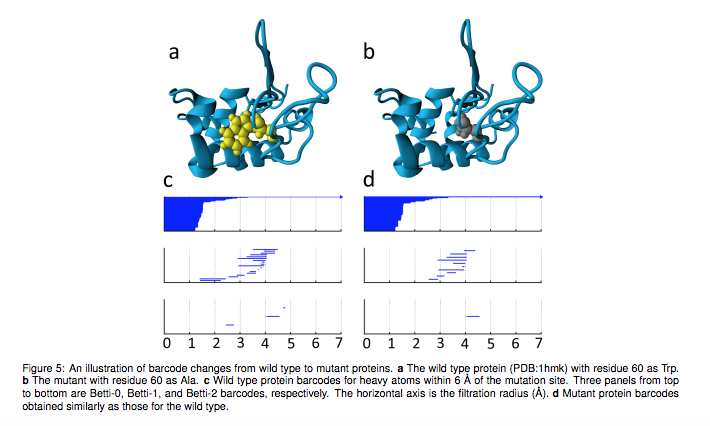
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
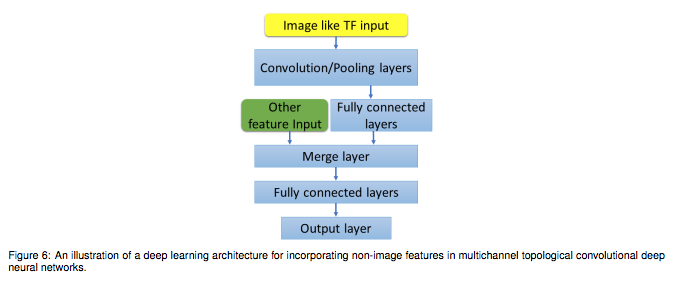
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
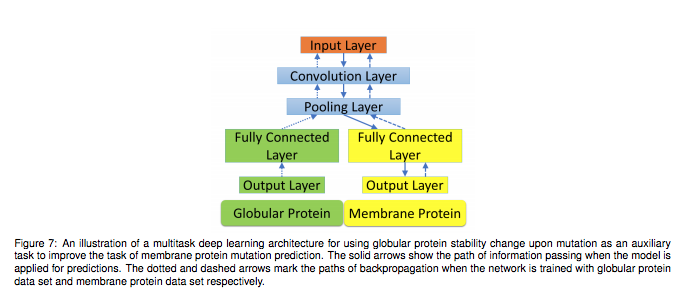
Zixuan Cang et.al., Topological based deep convolutional neural networks for biomolecular property predictions, Arxiv, 2017より転載。
次の論文は、生体分子に対して、multi-component persistent homolpogy ないしは multi-level persistent homologyを用いた機械学習モデルを提案するものです。
この論文は、従来のpersistent homology手法では、図形データからpersistent homologyを算出する際に、物質がもつ重要な化学的な性質が抜け落ちてしまうのに対して、multi-level persistent homologyを用いると、そのような重要な性質を漏らさず、persistent homologyに取り込むことができると主張しています。
同論文によると、従来のpersistent homology手法では、図形データからpersistent homologyを算出する際に、物質がもつ重要な化学的な性質が抜け落ちてしまうのに対して、multi-level persistent homologyを用いると、そのような重要な性質を漏らさず、persistent homologyに取り込むことができるようです。
また、従来のpersistent homology手法では、図形データからpersistent homologyを算出する際に、物質がもつ重要な化学的な性質が抜け落ちてしまうのに対して、multi-level persistent homologyを用いると、そのような重要な性質を漏らさず、persistent homologyに取り込むことができると、同論文は主張しています。
. In contrast to the conventional persistent homology, multi-component persistent homology retains critical chemical and biological information during the topological simplification of biomolecular geometric complexity.
Multi-level persistent homology enables a tailored topological description of inter- and/or intra-molecular interactions of interest.
なお、multi-level PHデータを入力値として受け取ることが機械学習器としては、(Random Forestモデルなどの)決定木のアンサンブル学習モデルや、畳み込みニューラル・ネットワークモデルなど、機械学習器としておなじみのモデルを選択できるという見解が提示されています。
These topological methods are paired with Wasserstein distance to characterize similarities between molecules and are further integrated with a variety of machine learning algorithms, including k-nearest neighbors, ensemble of trees, and deep convolutional neural networks, to manifest their descriptive and predictive powers for protein-ligand binding analysis and virtual screening of small molecules.
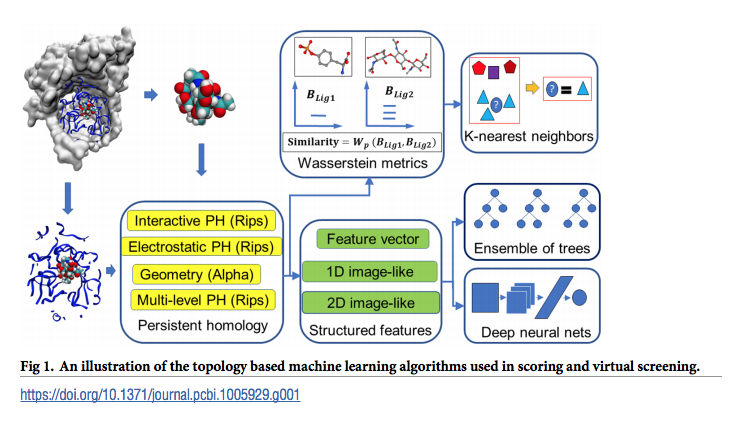
Zixuan Cang et.al., Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Computational Biology, January 8, 2018より転載。
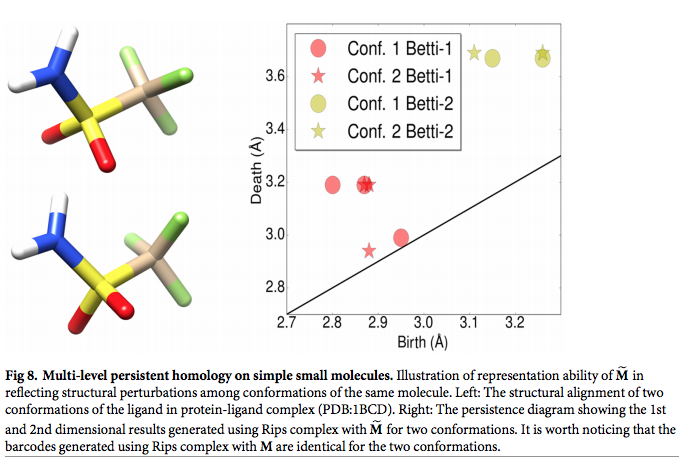
Zixuan Cang et.al., Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Computational Biology, January 8, 2018より転載。
以下は、畳込みニューラル・ネットワークモデルの畳み込み層の重み係数を、ヒートマップ表現で可視化したものです。Conv層にあるそれぞれのカーネルごとに、(学習の結果)どのような特徴が捉えられているのかが可視化されています。
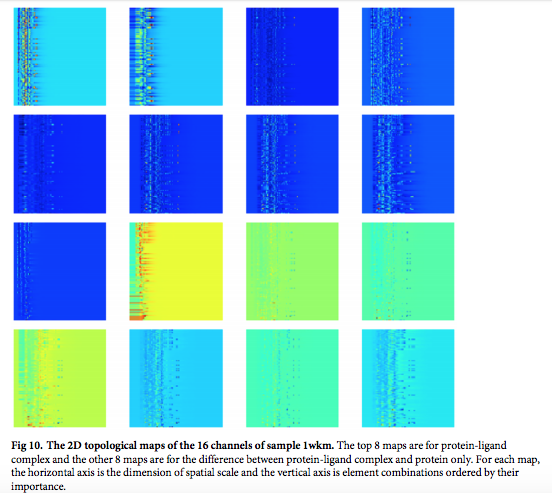
Zixuan Cang et.al., Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Computational Biology, January 8, 2018より転載。
以下が、提案モデルのアーキテクチャ図です。一番下にある入力層で受け取ることができるデータが、それぞれ異なることに注目してください。
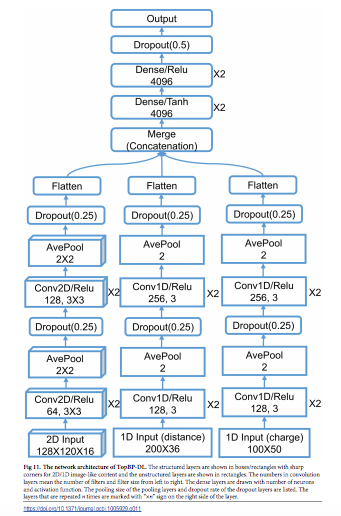
Zixuan Cang et.al., Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Computational Biology, January 8, 2018より転載。
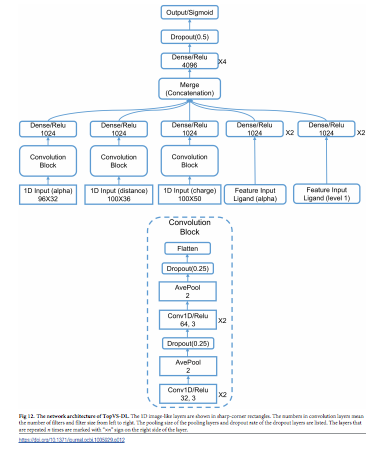
Zixuan Cang et.al., Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Computational Biology, January 8, 2018より転載。
タンパク質のデータ解析をPHを用いて行う世界
タンパク質のデータ解析をPHを用いて行う世界については、独立した文献として、以下があります。カーツワイル氏の唱えるGNR論のうち、「G」遺伝学と「N」ナノ・テクノロジーとが交差する領域で、PHをも用いた手法が可能であることを理解する上で、一つの参考になります。

PH ✕ CNNモデル: 「G」と「N」以外の領域での適用事例
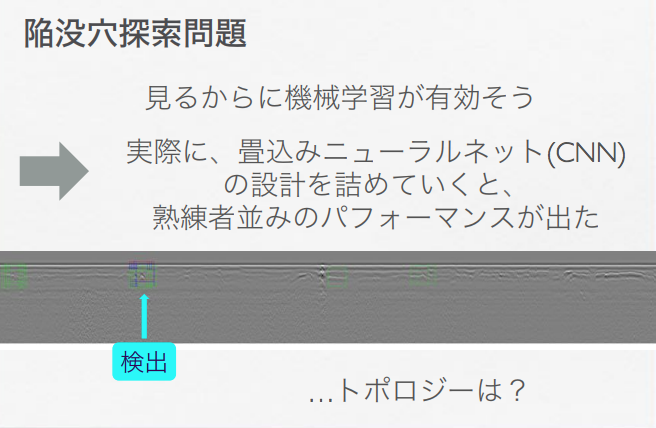
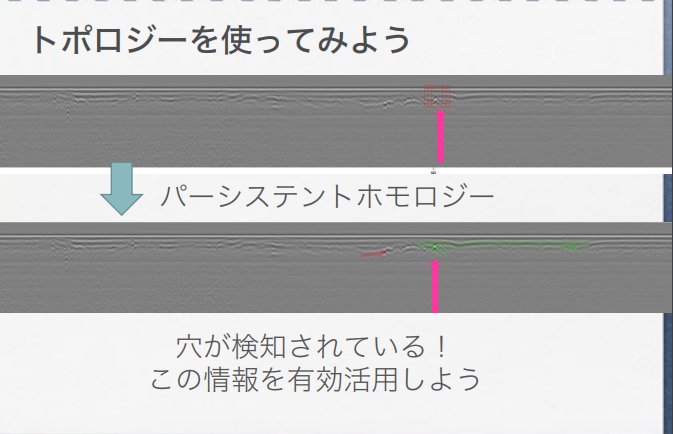
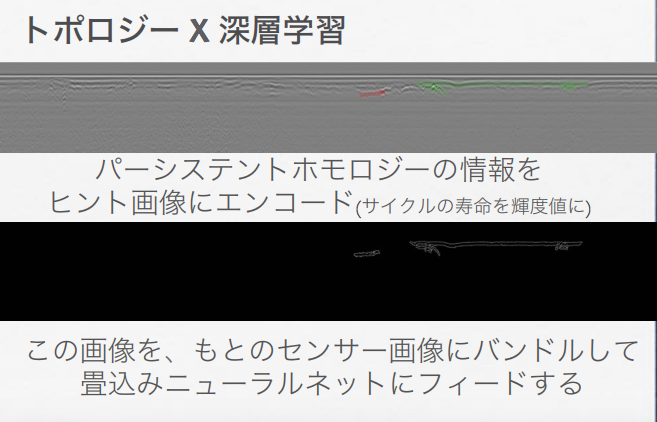
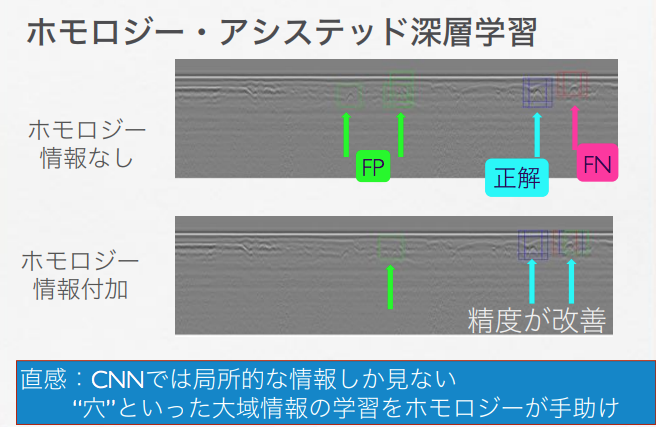
すでに取り上げた以下のスライドでは、道路上の陥没部分(穴があいた部分)をCNN(畳み込みニューラル・ネットワークモデル)で検出するタスクで、「CNNでは局所的な情報しか見ない。“穴”といった大域情報の学習をホモロジーが手助け」する役割を、PHは、CNNモデルに与えられることで果たすことができるのではないか、と論じています。

鍛冶 静雄「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
鍛冶 静雄「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
鍛冶 静雄「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
鍛冶 静雄「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
鍛冶 静雄「柔らかい幾何の拡がり -トポロジーの応用-」より転載。
研究が進んでいる計算トポロジー(Computational Topology)という領域
このように、「パーシステント図」や、「パーシステント図」によって可視化される「不変量」である「パーシステント・ホモロジー」を数理解析手法を用いて取り扱う領域は、「計算トポロジー」(Computational topology)と命名されています。
Algorithmic topology, or computational topology, is a subfield of topology with an overlap with areas of computer science, in particular, computational geometry and computational complexity theory.
A primary concern of algorithmic topology, as its name suggests, is to develop efficient algorithms for solving problems that arise naturally in fields such as computational geometry, graphics, robotics, structural biology and chemistry, using methods from computable topology.[1]
「計算トポロジー」アルゴリズム&専用解析ソフトウェア:トポロジーの「不変量」を数理的・計量的に取り扱うアルゴリズム
「計算トポロジー」について解説を加えているものとしては、以下がわかりやすいです。
2 計算トポロジーとは?
計算トポロジ ーとは,その名の通り, トポロジーで用いる不変量をコンピュータを用いて計算しようという理論のことである .
コンピュータは離散量しか扱えないため,空間そのものをデータとして入力することはできない .それでもコンピュータが有用なのは,前節のオイラー数の例のように ,空問を点や線といった構成要素に分解してその構造を組み合わせ的に表現し、その離散的な表現から不変量 を計算できるからである.
なかでもホモロジー群を計算するアルゴリズムは開発と実装が近年急速に進み,実用性が高まっている.
広く使われているソフトウェアパッケージとしてCHomP [4]が あるが,単体複体やビットマップ 画像など,様々なデータ構造を入力として用いることができる .
元々は力学系研究への応用を目指して開発されたパッケージであるため 、コンレイ指数など力学系の不変量を計算することもできる[1].詳しい使い方は[5]を参照されたい .
ホモロジー群の構 造を決定するためにはスミス標準形を用いて単因子を計算しなくてはなら ないが ,スミス標準形の計算アルゴリズムの計算量は行列のサイズに関して3 次のオー ダーであり,そのままでは高速とは言い難い ,
そこでホモロジー群の計算コストを下げるため,幾何学的な観察を用いて事前に空間を変形 するアルゴリズム が CHomPなどのホモロジー計算ソフトウェアには実装されている.
また、モース理論のアイデアを用いて逐次的にホモロジー群を計算するアルゴリズムなど,全 く別のアイデアも研究されている.
ホモロジー群を計算するアルゴリズムが盛んに研究されているのに比べ .それ以外の不変量 を計算するアルゴリズムはまだそれほど知られていない.(絡み目のlinkingnumberを計算す るアルゴリズム[6]はある).
「可換」な情報を引き出すホモロジーに比べると,「非可換」な不変量は格段に計算が難しい というのが 1 つの理由と思われる 。
計算トポロジ ーに関するテキストも揃い始めた.
基礎的なところから解説しているものとしてCHomPの開発者らによる[7]Persistent Homologyの提唱者らによる[8]、[9]などがある .
3 どの ように使うのか ?
計算ホモロジー理論は , どのような場面で , どのような目的に使えるのであろうか .
以下では幾つかの例を簡単に見ていこう,
3,1 形の違いを定還化したい
最も基本的なのは ,ホモロジー群が違えば空間が違うという性質を用いて ,空間の分類をす るという使い方である。
上記の引用文中で注が付されている部分がありますが、論考末尾に掲載されている注釈文は以下になります。
- [7] Kaczynski,T., Mischaikow,K.and Mrozek,M., Computational Homoiogy. Springer−Veriag. 2004.
- [8] Zomorodian,A,J., Topology for Computing,Cam bridge Univ.Press,2005.
- [9] Edelsbrunfier,H.and Harer,J.L., Computatinal Topology : An Introduction ,American Mathematical Society,2010
また、文中で挙げられているソフトウェアであるCHomPは、同名の名称を冠せられた研究プロジェクトであるHomP: Computational Homology Projectのなかで開発されたソフトウェアのことです下。
CHOMP: The Original CHomP SoftwareのWeb pageのトップページ
このソフトウェアの解説資料としては、以下があります。
1 はじめに ホモロジー群計算ソフトウェア CHomP はホモロジー群の計算機を用いた高速計算,及びその応用を目指したプロジェクト Computational Homology Project [3] によって開発された. 現在サポートしている OS は Windows,Mac,Unix,Linux であり,ウェブページ [3] からダウンロード可能である.
ここで主に扱う幾何的対象は方体集合と呼ばれる区間の直積で構成されるものであり,そのデータ構造の特徴(三角形分割を必要としない)から様々な分野への応用が展開されている. そこで本稿では CHomP の基本的な扱い方について解説を試みる.
特に,頻繁に使われるいくつかのコマンドの入出力関連についての説明を中心に進めていく. インストール方法についてはウェブページ [3] 内にプログラム開発者による詳しい解説があるのでここでは省略する. ちなみにこのウェブページにはここでは取り扱わないコマンドの使用法,豊富な例題,様々な応用例等の有益な情報が公開されているので一読をお勧めする.
まず始めに2節で単体複体のホモロジー群,3 節で方体集合のホモロジー群についてのCHomP による扱い方を説明する.
CHomP では方体集合間のあるクラスの連続写像に対してその誘導準同型写像を計算することが可能であり,それに関する解説を4節にまとめた.
最後の5節では C++インターフェースについて基本的な使用方法を紹介している.
なお方体集合のホモロジー群については文献 [1] に詳しく解説されているので参照されたい.
なお、同ソフトウェアのソースコードは、GitHubにアップロードされて公開されています。(リポジトリ名:shaunharker/CHomP)興味のある方は、コードを落としてコマンドを叩いてみてみることができます。
その他、R言語のライブラリ管理環境であるCRANに格納されているライブラリなどについては、以下を参照ください。
さらに以下のスライドでは、次の4つのソフトウェアが紹介されています。
- Perseus
- JavaPlex
- Dipha
- GUDHI
「パーシステント図」(PH)のベクトル表現 & カーネル埋め込み手法
「パーシステント図」を、高次元のベクトル空間内に、特徴ベクトルとして写像する手法や、カーネル埋め込みを行う手法については、すでに取り上げましたが、補足として、2つのスライドを紹介します。
この手法を解説したスライドとしては、以下があります。
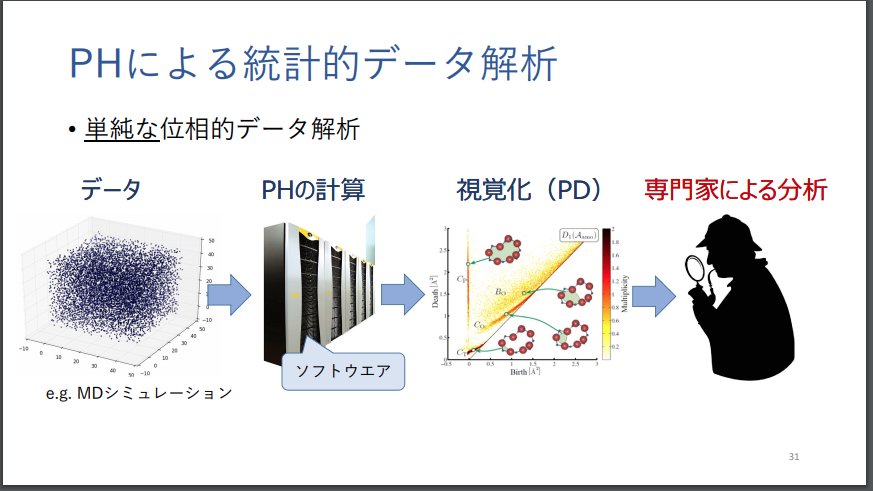
福水 健次 「パーシステント図に対する統計的機械学習」より転載。
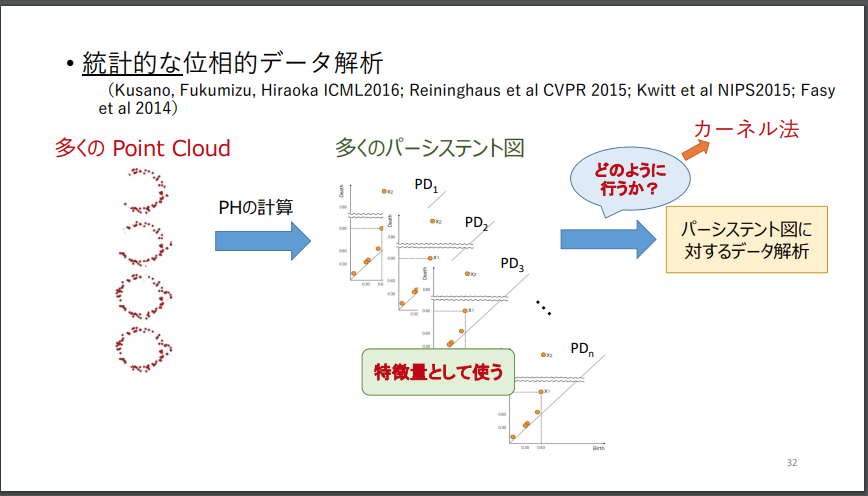
福水 健次 「パーシステント図に対する統計的機械学習」より転載。
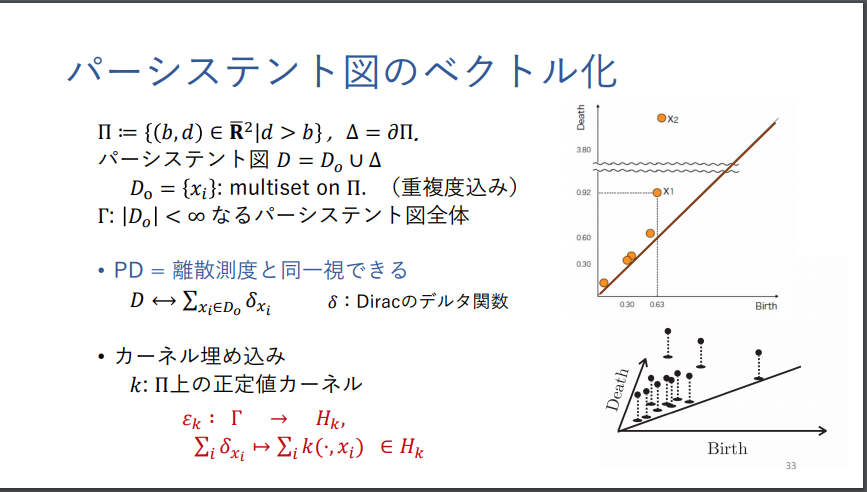
福水 健次 「パーシステント図に対する統計的機械学習」より転載。

福水 健次 「パーシステント図に対する統計的機械学習」より転載。

福水 健次 「パーシステント図に対する統計的機械学習」より転載。

福水 健次 「パーシステント図に対する統計的機械学習」より転載。
「パーシステント・ホモロジー」を統計論的機械学習のモデルを用いて解析する手法については、以下のスライドも参考になります。
TDAの適用事例と論文
以上、取り上げてきた手法は、TDA(Topological Data Analysis)と総称されています。
再び、以下よりスライドを転載します。

福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。

福水 健次 Persistence Weighted Gaussian Kernel for Topological Data Analysisより転載。
この手法を用いて、物質科学・ナノテクノロジーのデータ解析課題に取り組んでいる事例と論考としては、すでに取り上げたものを含めて、以下があります。
- 平岡 裕章・西浦 廉政 「ランダムの中に見る秩序―パーシステントホモロジーとその応用―」
- 統計数理研究所 統数研プロジェクト紹介 第8回 「物質科学への応用に向けた位相的統計理論の構築」トポロジーを応用した統計理論でソフトマターの構造解明を目指す
- 福水 健次(統計数理研究所 数理・推論研究系/統計的機械学習研究センター), Persistence Weighted Gaussian Kernel for Topological Data Analysis
- 平岡 裕章, Topological Data Analysis on Materials Science, 材料科学への位相的データ解析JST CREST 「ソフトマター記述言語の創造に向けた位相的データ解析理論の構築」
- Jeremy A. Pike1ほか, Topological data analysis quantifies biological nano-structure from single molecule localization microscopy
- RIKEN Center for Advanced Intelligence Project, Topological Data Analysis Team (Team Leader: Yasuaki Hiraoka (Ph.D.))
- 大林一平 (東北大学 原子分子材料科学高等研究機構) 位相的データ解析の現在
「位相」と「位相幾何学」とは?
数学上の「集合」の概念に、「位相」の定義(概念)を加えたものが「位相空間」であり、その「位相空間」にさらに「距離」の定義(概念)を加えたものが「距離空間」です。
ユークリッド空間は「距離空間」の一種になります。
数学上では、「集合」 → 「位相空間」 → 「距離空間」 と、左から右へ進むほど、その空間と空間における要素の関係について、定義された情報の量が大きく(豊かに)なります。 このあたりの事情は、以下が参考になります。
- Tomoki Kawahira(東京工業大学)「第3章 位相空間の基礎のキソ」
- 同上 「第4章 多様体の基礎のキソ」
- jamuojisan(2019年01月19日に更新)「位相空間の導入のために距離空間を理解する」
「パーシステント・ホモロジー」は、集合 → 位相空間 → 距離空間と拡大していく数学上の空間概念のうち、まんなか(2番目)の位相空間について数学者たちが開拓してきた知見を活用したものです。
なお、多層ニューラル・ネットワークモデルの隣り合う2層の間で、どのような情報圧縮がおこわれているかを、位相幾何学(トポロジー)の言葉を用いて理解しようとする試みもおこなわれています。
多層ニューラル・ネットワークモデルは、「多様体学習」(Manifold Learning)モデルの1つであると考えることができるため、こうした試みが可能となります。
- KojiOhki (2018/01/26) 「ニューラルネットワーク、多様体、トポロジー」
トポロジー(位相幾何学):Persistent homology以外の物質科学・物理学における活用事例
トポロジー(位相幾何学)には、Persistent homology以外にも、「結び目理論」(knot theory)と呼ばれる領域があります。
「結び目理論」(knot theory)は、生体分子を始めとする高分子物質の構造解析や、物理学の量子重力理論における「弦」の絡み合いの状況を解析するなど、自然科学の様々な領域で活用されているようです。
- 下川航也 (2016年8月) 「トポロジーと高分子」
- 河内明夫(大阪市立大学大学院理学研究科) 「結び目理論の科学への応用-プリオン分子モデルとこころのモデルを中心として」
- [スライド版] 河内明夫(大阪市立大学大学院理学研究科) 「結び目理論の科学への応用-プリオン分子モデルとこころのモデルを中心として」
このあたりの様子は、以下のスライドで概観されています。

玉木 大(信州大学理学部数理・自然情報科学科)「トポロジーは応用できるか?」, 日本数学会秋季総合分科会 市民講演会, 2011年10月1日より転載。

玉木 大(信州大学理学部数理・自然情報科学科)「トポロジーは応用できるか?」, 日本数学会秋季総合分科会 市民講演会, 2011年10月1日より転載。
遺伝情報解析におけるAI技術(2)〜 Deep Tensor Networkモデル
次は、Neural Tensor Network(Deep Tensor Network)を用いた取り組みです。
物質を、ナノ・スケール(1mのマイナス9乗のサイズ)の分子レベルや原子レベルで解析したり、原子・分子の結合配置を人為的に組み替えることで、人間の意図する機能と挙動を示す物質を人工的に生み出す技術が、ナノ・テクノロジーです。
このナノ・テクノロジーにおいて、原子や分子どうしの結合関係を解析する上で、「原子や分子どうしの結合関係」を分析する手法の1つに、Neural Tensor Network(Deep Tensor Network)モデルがあります。
この手法は、「テンソル代数」と呼ばれる数学で確立された「テンソル分解」(Tucker分解)の解を、従来行われてきた最小二乗法などのアルゴリズムを用いて近似解を求めるのではなく、深層ニューラル・ネットワークの誤差逆伝播法を用いて近似解を求めるアプローチです。
データ分析において、解析の遡上にのせている複数の事物(Entity)が持つ無数の「属性」のうち、任意の2種類の「属性」(property)を取り出して、「物質A」がもつ「属性1」と「物質B」がもつ「属性2」の間に、どのような関係が成立しているのかを、2次元の表形式のデータシート(Relational Database System(RDMS)内のtable)で、行列(matrix)形式で表現することができます。
マーケティング分析の例を挙げると、顧客は例えば、以下のような「属性」を持ちます。
- 「年齢区分」
- 「来店頻度」
- 「来店時間帯」
- 「来店あたりの購入総額単価」
- 「購入商品カテゴリ」
- ・・・
次元数(数学上の概念としては、「階数」)が「2」の行列表現では、上記のような(データ解析の対象エンティティがもつ)無数の「属性」のうち、2つの属性を選び出して、事物がもつ2つの属性の間の関係を、表現することができます。
これに対して、「スカラー」と「ベクトル」、「行列」を拡張した数学上の概念である「テンソル」を用いると、数学の世界では、対象とする複数の事物が持つ無限種類の「属性」間の関係を表現することができます。
この無限個の関係を格納(表現)した「テンソル」を、行列における低ランク分解(次元圧縮)に相当する「テンソル分解」の演算操作を加えて、データ解析によって浮かび上がらせたい何らかの着目すべき(事物間の)(特定の)関係を表現(格納)した、より次元数の低い「コアテンソル」を得ることができます。
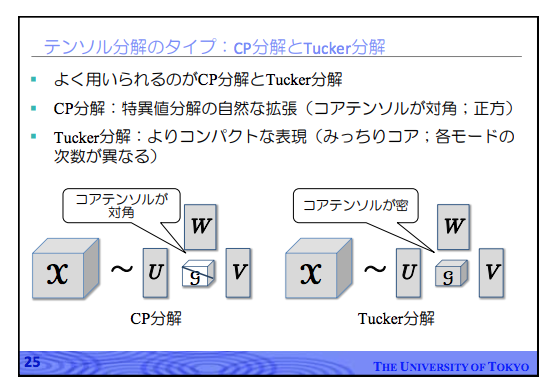
テンソル分解で広く用いられているTucker分解については、以下のスライドの次の図表が分かりやすいです。
テンソル形式(型)のデータをテンソル分解することで、元のテンソル形式のデータよりも次元数の低い「コア・テンソル」と呼ばれる低ランク・テンソルを得る方法について、[スライド版] 鹿島 久嗣 「関係データの機械学習 -行列・テンソル分解によるアプローチ -」から以下のスライドを転載します。
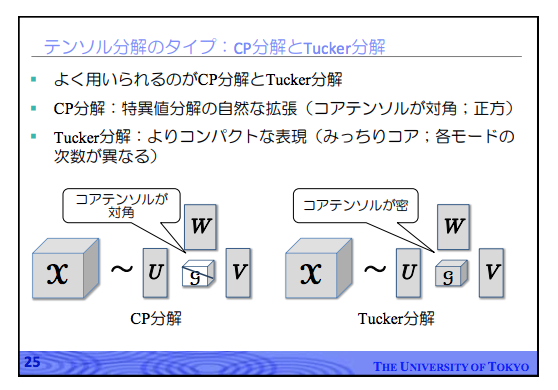
[スライド版] 鹿島 久嗣 「関係データの機械学習 -行列・テンソル分解によるアプローチ -」より転載。
この「テンソル分解」を行う際に、もっとも広く行われているのはTucker分解という手法ですが、冒頭で取り上げる富士通の事例では、事物(Entity)どうしの「つながり」関係を表現したテンソル型のデータから、従来の「テンソル分解」によって、(次元数の小さい「コア・テンソル」に)「つながり」を表現させるだけでなく、何らかの観点から「分類」しやすいような「つながり」を「コア・テンソル」に写像することを目指しています。
富士通の取り組み事例:Deep Tensor モデル
富士通は、テンソル分解によって「コア・テンソル」を算出する際に、算出される「コア・テンソル」のなかに、機械学習モデルによって「分類」されやすい性質をもつ「つながり」が情報保存されるようにするために、従来のテンソル分解に対して、拘束条件(制約条件)を加える「構造制約テンソル分解」という独自の手法を考案したようです。
(富士通)「構造制約テンソル分解」(SRTD)
- [プレス・リリース](2016年10月20日) 株式会社富士通研究所 「人やモノのつながりを表すグラフ構造のデータから新たな知見を導く新技術「Deep Tensor」を開発」
- 富士 秀ほか 「Deep Tensorとナレッジグラフを融合した説明可能なAI」
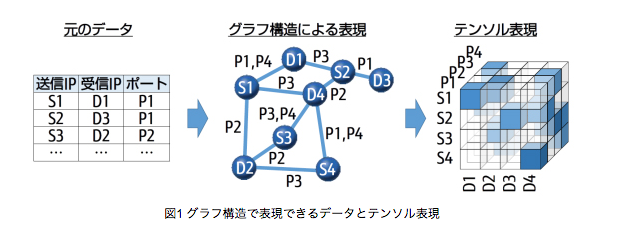
富士通プレス・リリースより、図1を転載。
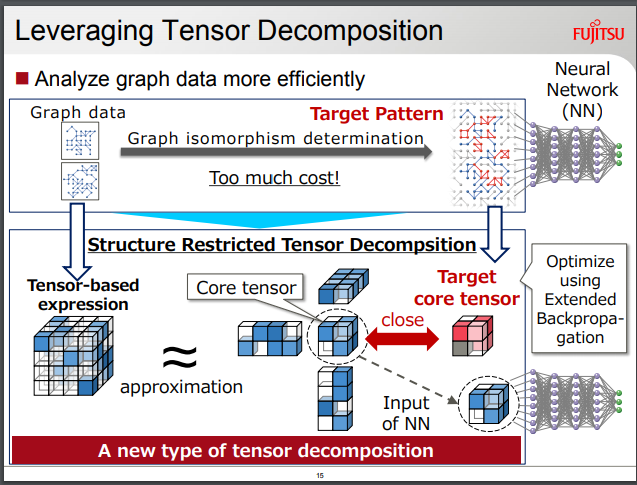
FUJITSU LABORATORIES LTD.(25th April 2018)Explainable AI that Can be Used for Judgment with Responsibilityより転載。

FUJITSU LABORATORIES LTD.(25th April 2018)Explainable AI that Can be Used for Judgment with Responsibilityより転載。
Deep Tensor:「構造制約テンソル分解」器と深層ニューラル・ネットワークモデルの結合
この「構造制約テンソル分解」(SRTD: Structure Restricted Tensor Decompsition)の出力結果は、テンソル分解器に入力させた元のグラフ形式のデータがもつ特徴を、うまく(低ランクのコア・テンソルに)圧縮したものになります。
富士通が提案するDeep Tensorモデルは、SRTDの出力結果を、分類タスクを処理する深層ニューラル・ネットワークモデルに入力させるアーキテクチャになります。
Deep Tensorモデルは、「構造制約テンソル分解」演算器を前段部にもち、(「つながり」を分類するための)分類器である深層ニューラル・ネットワークモデルを後段にもつ、2段構えのアーキテクチャーで構成されるものです。
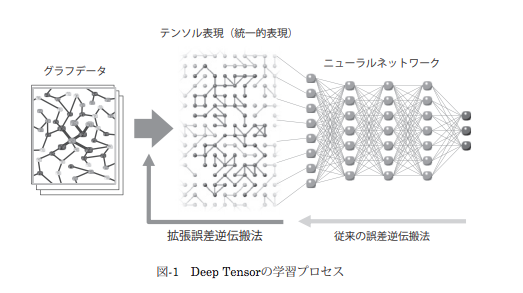
富士 秀ほか 「Deep Tensorとナレッジグラフを融合した説明可能なAI」より転載。
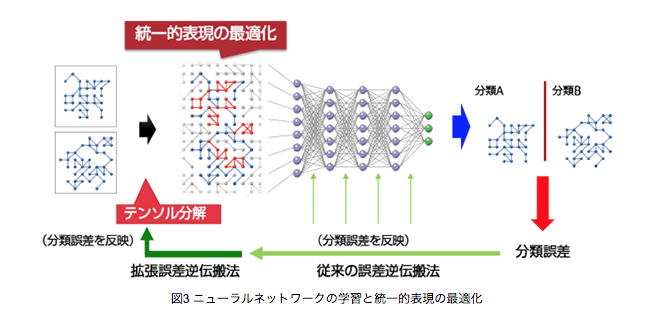
「(2016年10月20日) 株式会社富士通研究所 プレス・リリース 人やモノのつながりを表すグラフ構造のデータから新たな知見を導く新技術「Deep Tensor」を開発」より転載。
後段の深層ニューラル・ネットワークモデルは、「コア・テンソル」のなかに表現された「つながり」をもとに、対象データ集合(事物の集合)の内部で成立している「つながり」関係を分類するもので、ディープ・ラーニングモデルとして、誤差逆伝播法で学習を行うものです。
このDeep Tensor モデルについては論文が出ていないようですが、富士通研究所からは以下の論文がでており、この論文のなかで、「構造制約テンソル分解」とDeep Tensor モデルについても言及されています。
以下、上記の論文の一節を引用します。なお、太線部と斜線部、および下線部は小野寺によるものです。
However, a core tensor calculated with conventional tensor decompositions only expresses structures learnt in an unsupervised manner, and they are not necessarily the important structures for the classification of data. To tackle this problem, we propose DeepTensor leveraged by Structure Restricted Tensor Decomposition (SRTD), a novel type of tensor decomposition.
SRTD uses a tensor called the target core tensor, which contains the aggregated structures that are important for classification and guides the tensor decomposition into more effective results.
We also introduce the extended backpropagation (EBP) algorithm, which learns the optimal target core tensor along with the parameters of the neural network.
Moreover, once we know the indices of the core tensor important for the classification results, we can interpret them in terms of the indices of the input tensor by using the factor matrices, which can connect between the indices of the input tensor and those of the core tensor.
We report on the experimental results on three different domains: intrusion detection, peer-to-peer (P2P) lending, and bioinformatics.
We empirically show that our method is highly accurate, especially on higher order data, while enabling us to interpret the classification results.
(富士通)「拡張誤差逆伝播法」
このモデルを学習段階で学習させる際には、モデルが推論した分類ラベルの推定結果と、教師用正解データとの「誤差」をもとに、モデルの内部パラメータを最適化させますが、通常の深層ニューラルネットワーク・モデルに結合されている前段部の「構造制約テンソル分解」器の内部パラメータにまで、後段の多層ニューラルネット・モデルの出力層から逆伝播してきた「誤差」を(逆)伝播させていくところが、通常の誤差逆伝播法(BP法)と異なります。
富士通は、この方法を、「拡張誤差逆伝播法」と命名しています。
Deep Tensor モデルは、このような「拡張誤差逆伝播法」によって、後段の深層ニューラル・ネットワークの内部パラメータと、前段の「構造制約テンソル分解」器の内部パラメータの両者を、end-to-endに一括して同時に最適化させるアプローチをとるようです。
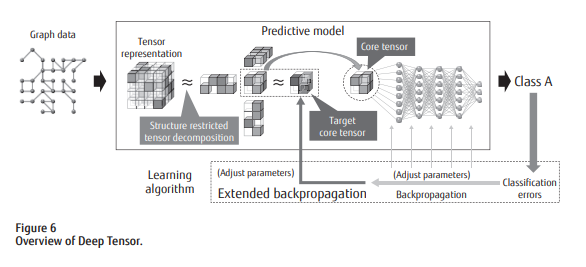
Koji Maruhashi, Deep Tensor: Eliciting New Insights from Graph Data that express Relationships between People and Things, FUJITAS Sci. Tech. J., Vol.53, No.5, pp26-31 (September 2017)より転載。
(富士通)結論に至った過程が「説明可能」なAI:ドメイン構造知識データをさらに参照させる
富士通は、このDeep Tensorモデルを学習後に、推論段階で運用させる際に、とりくむタスクのドメイン領域に特化したグラフ形式の「知識データ」を参照させることで、モデルが分類結果を出力した際の判断根拠を、人間が目でみて解釈することができるようにする「説明可能なAI」を構築したと発表しています。
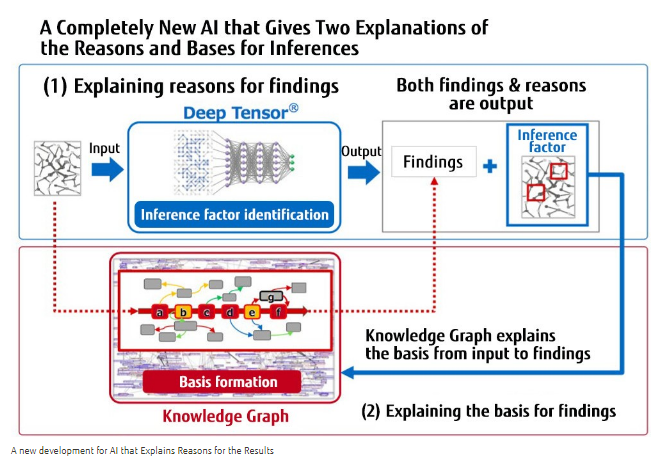
FUJITSU JOURNAL (October 11, 2018) Explainable AI Accelerates Digital Transformation in the Financial Services Industry, Enhancing Risk Management and Other Operationsより転載。
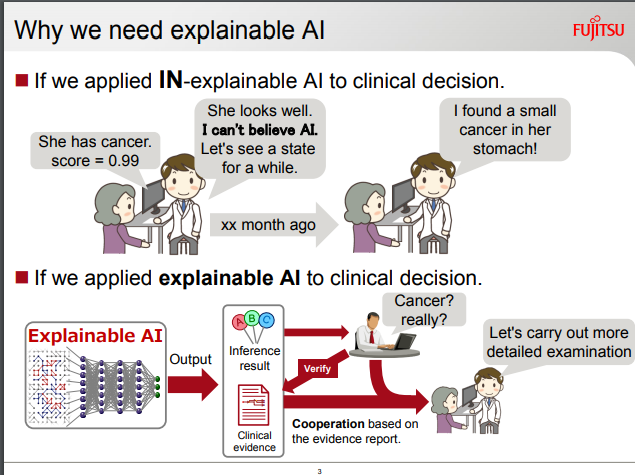
FUJITSU LABORATORIES LTD.(25th April 2018) Explainable AI that Can be Used for Judgment with Responsibilityより転載。
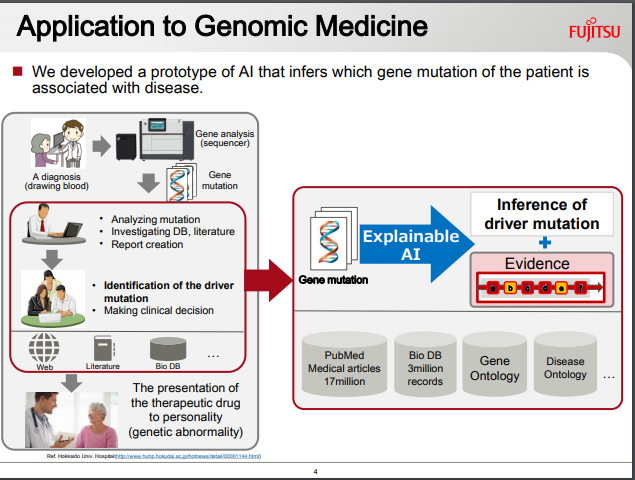
FUJITSU LABORATORIES LTD.(25th April 2018) Explainable AI that Can be Used for Judgment with Responsibilityより転載。
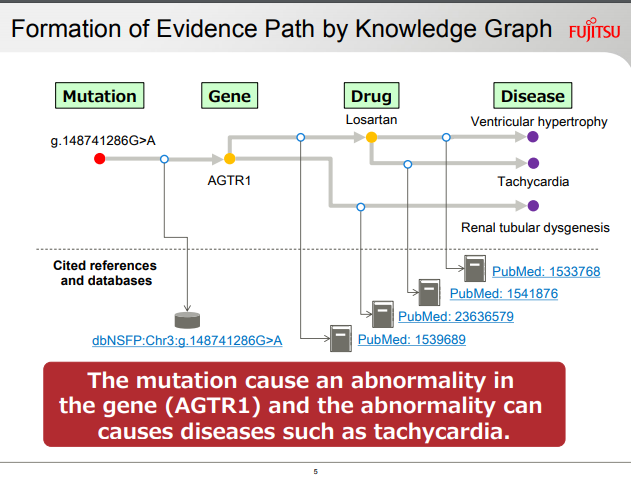
FUJITSU LABORATORIES LTD.(25th April 2018) Explainable AI that Can be Used for Judgment with Responsibilityより転載。

FUJITSU LABORATORIES LTD.(25th April 2018) Explainable AI that Can be Used for Judgment with Responsibilityより転載。

FUJITSU LABORATORIES LTD.(25th April 2018) Explainable AI that Can be Used for Judgment with Responsibilityより転載。
富士通はこのモデルを、インターネット・ネットワークへの外部からの不正侵入の検出タスクと、分子結合構造形状の解析タスクの2つのタスクで試すことで、精度検証を行ったようです。
後者の物質解析タスクは、「原子(元素記号ラベル付き)間の結合関係を表すグラフの構造」が表現されたデータセットであるスイス連邦工科大学チューリッヒ校(ETH zurich)のデータを入力値として、毒性や活性を予測する」課題を含む複数の課題を行ったようです。
富士通のプレス・リリースでは、精度検証試験を行った結果、Deep Tensorモデルを適用し、いずれの課題に対しても、従来手法を上回る分類精度を得られたことが報告されています。
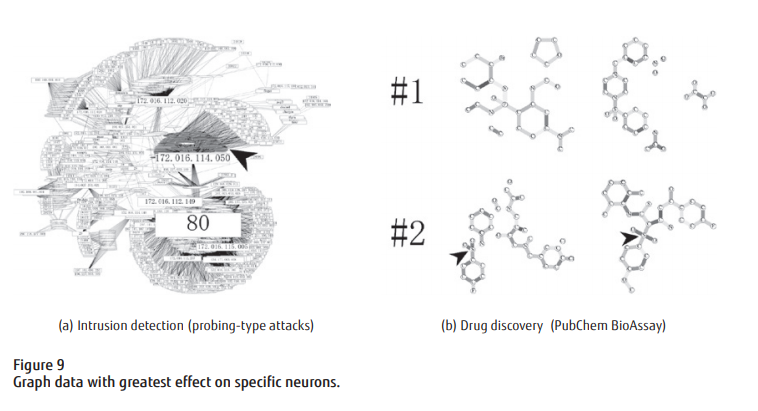
Koji Maruhashi, Deep Tensor: Eliciting New Insights from Graph Data that express Relationships between People and Things, FUJITAS Sci. Tech. J., Vol.53, No.5, pp26-31 (September 2017)より転載。
(参考)判断根拠(内部処理)の可視化技術:通常の深層学習モデルの場合
富士通のDeep Tensorでは、AIモデルが分類結果を出力するに至るまでのデータの内部処理過程(判断根拠)を、人間が目視確認できると、プレス・リリースでは解説されていました。
モデル内の内部処理過程を人間が確認できるようにすることで、モデルがどのような判断根拠に基づいてアウトプットを出すに至ったのかを確認する術を得る方法については、従来の深層ニューラル・ネットワークモデルに関しても、CAM: Class Activation Mapとよばれる手法や、同手法の改良手法であるGrad-CAM: Guided CAMなどの手法が提案されています。
これらの可視化手法は、畳み込みニューラル・ネットワークを対象とするものです。
- icoxfig417 「ディープラーニングの判断根拠を理解する手法」
- Platinum Data Blog(2017/07/10)「深層学習は画像のどこを見ている!? CNNで「お好み焼き」と「ピザ」の違いを検証」
RNNやLSTMなどの時系列深層学習モデルについては、以下の手法が提案されています。
- Visualizing LSTM Networks. Part I. Australian sign language model visualization.
- Jos van der Westhuizen & Joan Lasenby, Visualizing LSTM decisions, Arxiv, 2018
- LASTMVis – Visual Analysis for Recurrent Neural Networks
- Hendrik Strobelt et.al., LSTMVis: A Tool for Visual Analysis of Hidden State Dynamics in Recurrent Neural Networks
- Jos van der Westhuizen & Joan Lasenby, Techniques for visualizing LSTMs applied to electrocardiograms, 2018 ICML Workshop
なお、分類モデルや予測モデルの判断根拠(出力値に至るまでのデータ処理過程)を可視化する目的とは、やや趣きを異にするものとして、人間がいろいろな事物を目にするときに、対象となる物体のどこに視線を向けてその物体を認識しているのかを可視化する以下の取り組みもあるようです。
In this paper, we follow the basic idea of GAN and propose a novel model for image saliency detection, which is called Supervised Adversarial Networks (SAN).
Specifically, SAN also trains two models simultaneously: the G-Network takes natural images as inputs and generates corresponding saliency maps (synthetic saliency maps), and the D-Network is trained to determine whether one sample is a synthetic saliency map or ground-truth saliency map.
However, different from GAN, the proposed method uses fully supervised learning to learn both G-Network and D-Network by applying class labels of the training set.
深層ニューラル・ネットワークモデルは長らく、内部のデータ処理過程が人間からみて「ブラック・ボックス」であり、どのような判断根拠に基づいて分類結果や予測結果を(モデルが)人間に提示しているのか、モデルの側から説明が得られない、という欠点が指摘されてきました。
この「欠点」があだとなり、医療や交通管制システム、金融など、人間の命や経済的利益(損失)を始め、人々の生活基盤を支えるライフラインまわりで、深層学習モデルを利用することがためらわれる傾向がありました。こうした事情は、すでに取り上げた富士通のスライドでも述べられているとおりです。
モデルの内部処理過程(特定の結果に至った判断根拠)を説明できる仕組みを備えたAIモデルが、今後、データ処理器として、産業界の主流を占めてくるのかもしれません。
では、本題に戻ります。
テンソル分解 ✕ 深層ニューラル・ネットワークモデル:Deep Tensor 以外の例
この「テンソル分解」と深層ニューラル・ネットワークモデルを組み合わせたアーキテクチャーはは、Deep Tensor Neural Netowks モデルとも呼ばれています。
富士通のDeep Tensorは、このDTNNモデルの1種に分類することができます。
富士通のDeep Tensor以外のDTNNモデルの事例としては、例えば以下があります。
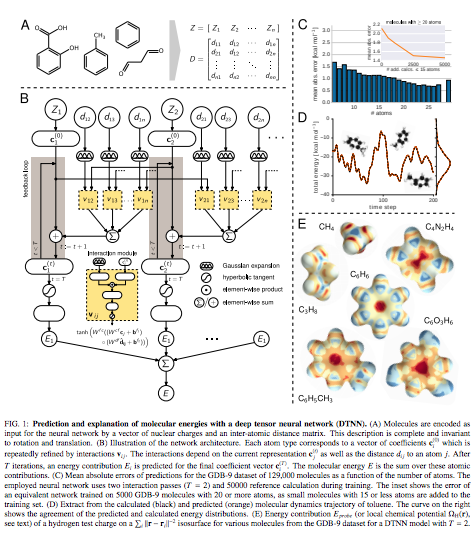
Kristof T. Schuttほか(2016), Quantum-Chemical Insights from Deep Tensor Neural NetworksよりFig.1を転載。
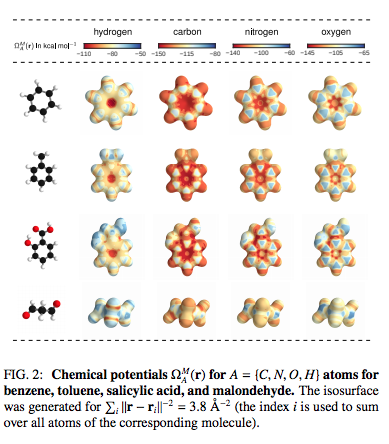
Kristof T. Schuttほか(2016), Quantum-Chemical Insights from Deep Tensor Neural NetworksよりFig.2を転載。
この論文の実装コードを収録したGitHubリポジトリは、以下になります。
DTNN: Deep Tensor Neural Networksの一例として、テンソル分解器の後ろに、畳み込みニューラル・ネットワークモデル(CNN:Convolutional Neural Network)を結合させたモデルを、量子化学(quantum chemical)のデータ解析に適用した事例としては、以下の論文があります。
この論文を解説したスライドとしては、DeNA社のKazuki Fujikawa氏による次のスライドがあります。
- [解説スライド] Kazuki Fujikawa, SchNet: A continuous-filter convolutional neural network for modeling quantum interactions
- Yoav Levine et.al.(2018), Bridging Many-Body Quantum Physics and Deep Learning via Tensor Networks
もとになったのは、関係データ分析の手法である「テンソル分解」
このNeural Tensor Network (Deep Tensor Network)モデルは、任意の2つの事物(エンティティ:Entity)の間に成立する関係性を推定したり、分類したりする関係データ分析(Relational data modeling)に有効な手法として知られてきたテンソル分解と呼ばれる数学演算手法を、ニューラル・ネットワークで表現したモデルになります。(テンソル分解を用いて関係データを分析するデータ解析手法は、数学のテンソル(Tensor: スカラーとベクトルよりも次元数の大きい数学的実体を表現する数学上の概念)を用いるものです)
テンソル分解で広く用いられているTucker分解については、以下のスライドの次の図表が分かりやすいです。
[スライド版] 鹿島 久嗣 「関係データの機械学習 -行列・テンソル分解によるアプローチ -」より転載。
数学におけるテンソル代数
なお、このようなテンソルについて数学的にきちんと理解するためには、「テンソル代数」を学ぶ必要があります。
この「テンソル代数」については、以下のオンライン・テキストが参考になります。
このテキストでは、テンソル代数に「交代性」という性質を織り込む(付加する)と「外積代数」という別の代数構造を組成することや、「双対性」や「ホッジ作用素」など、現代数学の(数学的な)構造を深いところで規定している鍵概念について、最初のイメージを視覚的につかむことができます。
数学の概念世界では、多重線形性をもつ「代数構造」や、「交代性」をもつ「代数構造」など、さまざな構造をもつ代数系が、閉じた系として成立可能であることが、上記のテキストと向き合うことで、垣間見ることができます。
以下は、物理のかぎしっぽ > 微分形式 > 外積代数の脚注からの引用です。
あとで見るように,実際,外積空間はテンソル空間に『積の交代性』という性質をつけ加えることで作ることが出来ます.テンソル代数の視点からは,外積代数のことを『交代形式のテンソル代数』と見ることが出来ます.
「外積代数」と「テンソル代数」との関係については、以下でも平易に整理されています。
以下、上記のウェブページから、ベクトル空間のなかで成立するそれぞれの代数系の関係が整理された図を転載します。
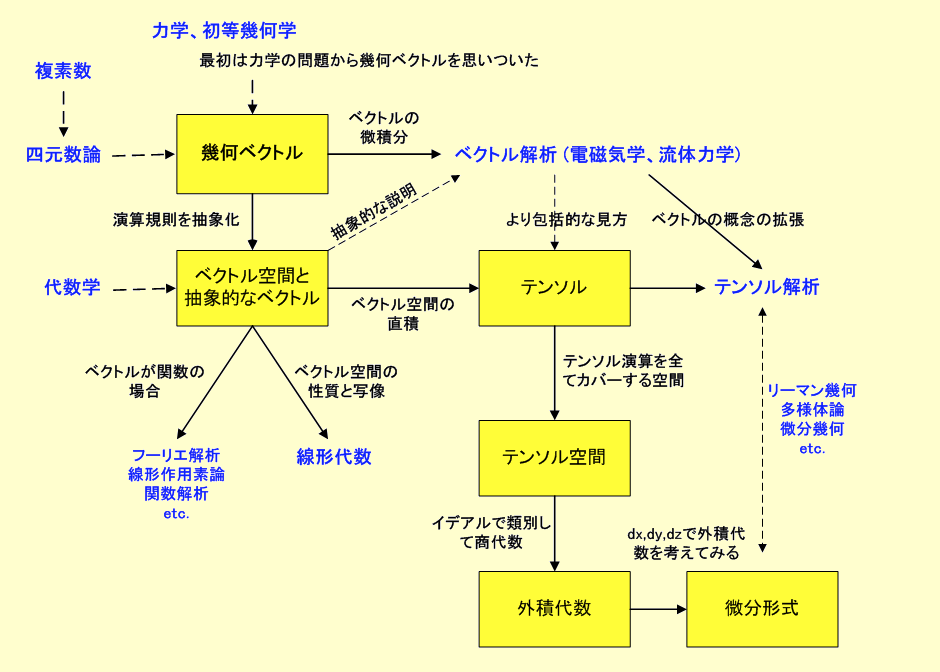
物理のかぎしっぽ 「イデアルで外積代数を入れる1」より転載。
このようなさまざまな代数系がもつ構造を、さらに「群論」や「圏論」の視覚から考察すると、「モノイド圏」ないしは「テンソル圏」などのさらに一段深い世界を見ることができます。
ベクトル空間、アーベル群、R–加群、R–多元環などの間に定義される通常のテンソル積は、それぞれの概念に付随する圏にモノイド構造を与える。ゆえにモノイド圏をこれら、あるいは他の例の一般化として見ることもできる。
(中略)
モノイド圏は圏論以外の分野において多数の応用を持つ。直観的線型論理の multiplicative fragment のモデルを定義し、物性物理学においてトポロジカル秩序相の数学的な基盤を与え、組み紐モノイド圏は場の量子論やひも理論に応用をもつ。
上記の引用文中、中略部分を挟んだ後段の記述は、数学における代数構造と圏論と、物理学における「場の量子論」や「ひも理論」と、数理論理学(「直観論的線型論理」)といった、数学・物理学・論理学の3者が、深いところでつながりあっている(通底している)世界観を示唆しています。
このあたりは、数学・物理学・論理学の3者が、深いところでつながりあっている可能性を示唆している「ラングランズ・プログラム」を考える際にも、手がかりとなるなんらかの光を差し込んでいるように思います。
なお、本連載記事のテーマからは外れますが、テンソル代数を理解することで、座標変換に対して「不変」である「不変量」を定義することができます。
物理学の中で、この座標変換に対する「不変性」をもった「物理量」を獲得することが不可欠である領域が、依拠する座標系によって物理量の観測値が変わってしまう(異なる複数の座標系の間で、同一の物理量の観測値が一致しない)世界を取り扱う「一般相対性理論」です。
「一般相対性理論」を学ぶことは、ほぼ、「テンソル代数」(双対性の関係にある「反変ベクトル」と「共変ベクトル」の関係を含めて)を学ぶことに等しいとも言われています。
テンソル代数の学習のつまづきどころ:上付添字と下付き添字(ベクトルの反変と共変)の関係性について
なお、一般相対性理論を学習する上で、しばしばベクトルの上側につく添字(反変ベクトルであることを表している)と、ベクトルの下側につく添字(共変ベクトルであることを示す)の「計量テンソル」による変換がもつ(数学上と物理学上の)「意味」がわからない、という言葉を聞きます。
曰く、上付き添字と下付き添字の入れ替えには、数学上や物理学上の意味はあるのか? 添字を上方から下方へ、はたまた、下方から上方へ入れ替えるのは、人為的に定めた単なる記号規則にのっとったものでしかないのではないのか?という疑問です。
これについては、以下の解説が助けになります。
ここまでをまとめると・・・
基底に対して展開した成分 ・・・ 基底と逆の変換を受ける → 反変成分
双対基底に対して展開した成分 ・・・ 基底と同じ変換を受ける → 共変成分
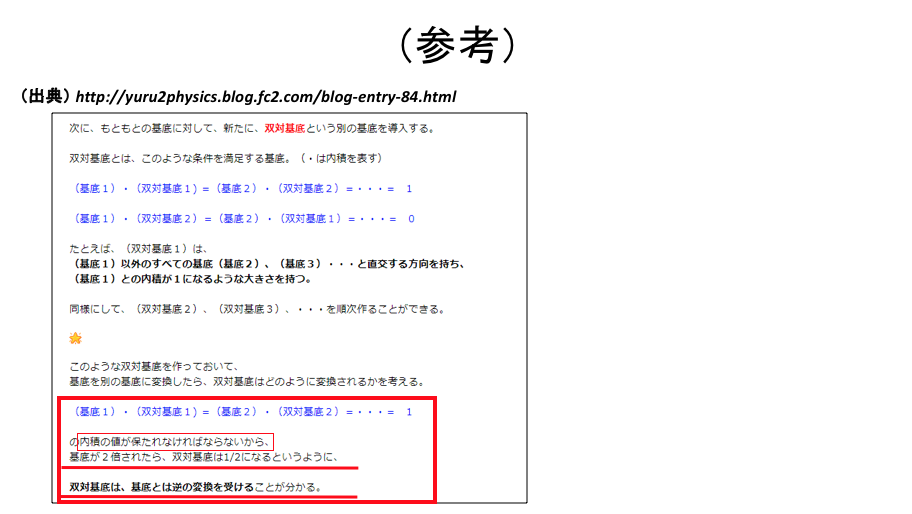
ゆるゆる物理☆ときどき数学 「共変と反変 (2)」より転載。赤枠と赤下線部は小野寺による。
このあたりをスライドに書き起こすと、次のようになります。
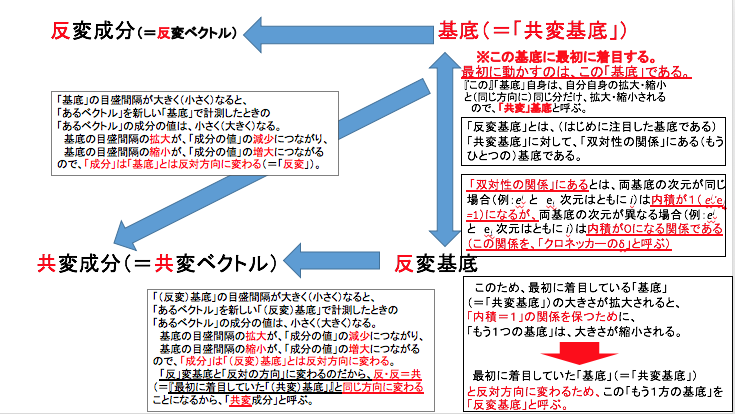
(小野寺作成スライド)
なお、このテンソル代数と外積代数の関係について、以下のような関係性についても、考えることもできるでしょうか。

(小野寺作成スライド)
以下のスライドでは、次のウェブページを参照しています。
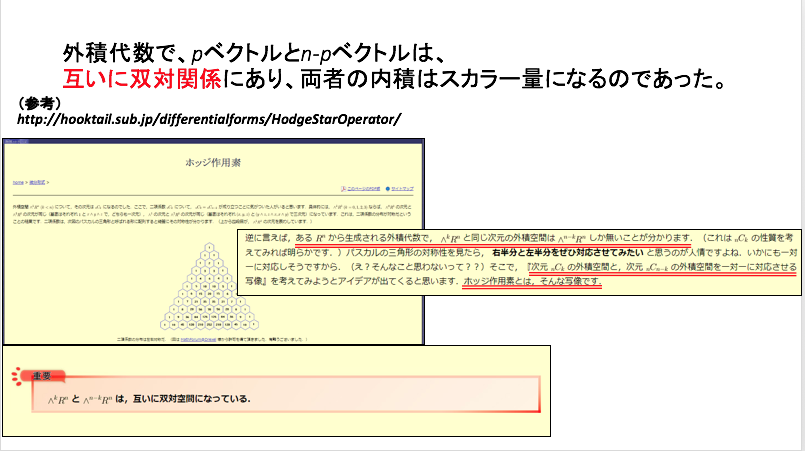
(小野寺作成スライド)
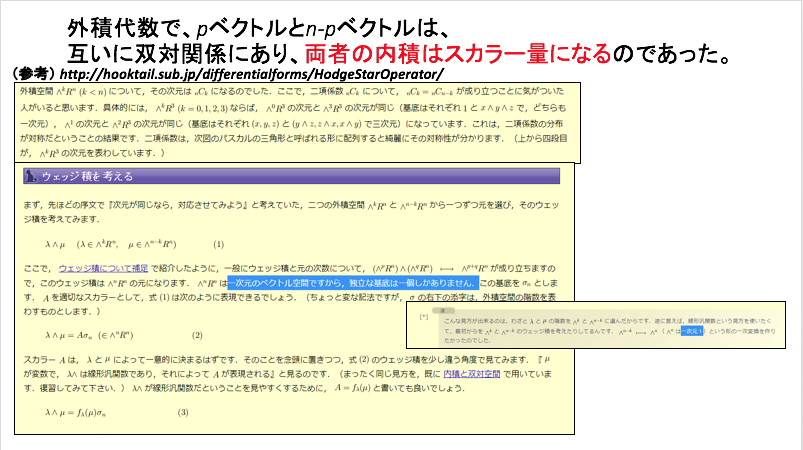
(小野寺作成スライド)

(小野寺作成スライド)
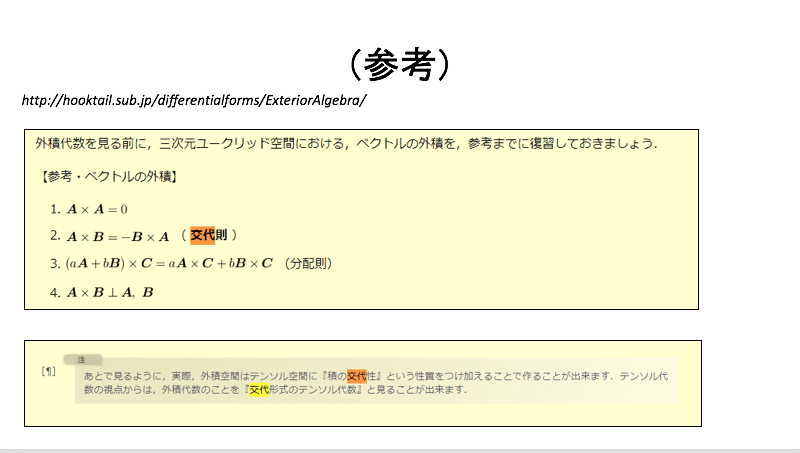
(小野寺作成スライド)
上記に登場する「ホッジスター作用素」(Hodge star operator)によって互いを行き来できる、(互いに)双対な2つの外積代数の空間は、「ホッジ双対」(Hodge dual)の関係にある、と定義されています。
以下、Wikipedia(日本語版)「ホッジ双対」より引用します。
数学において、ホッジスター作用素(ホッジスターさようそ、Hodge star operator)、もしくは、ホッジ双対(ホッジそうつい、Hodge dual)は、ホッジ(Hodge)により導入された線型写像である。ホッジ双対は、有限次元の向き付けられた内積空間の外積代数の上で定義されるk -ベクトルのなす空間からn-k-ベクトルのなす空間への線形同型である。
他のベクトル空間に対する多くの構成と同様に、ホッジスター作用素は多様体の上のベクトルバンドルへの作用に拡張することができる。 たとえば余接束の外積代数(すなわち、多様体上の微分形式の空間)に対して、ホッジスター作用素を用いてラプラス=ド・ラーム作用素を定義し、コンパクトなリーマン多様体上の微分形式のホッジ分解を導くことができる。
このように、現代数学のフィールドでは、さまざまな代数系のあいだに豊かな関係性が成立している様子が見えてきています。
(テンソル解析による)関係データ分析では、テンソルを用いて、データどうしの関係性を表現したり、テンソル分解を用いることによって、データ間の(複数の観点で成立している)関係性をデータ圧縮(低ランク近似)するといったことを行います。
このような(テンソル解析による)関係データ分析の背後に、上記でみてきたような現代数学の世界の空間が広がっていることに思いを馳せてみるのも、とても価値のあることであるかもしれません。
(脱線)一般相対性理論とテンソル
なお、座標変換に対する不変性(座標不変性)を担保するためには、テンソルの縮約によるスカラーの獲得が鍵概念になります。
縮約によって、もとのテンソルの階数(ランク)は、2つ小さくなります。
テンソルの「縮約」については、以下が分かりやすいです。
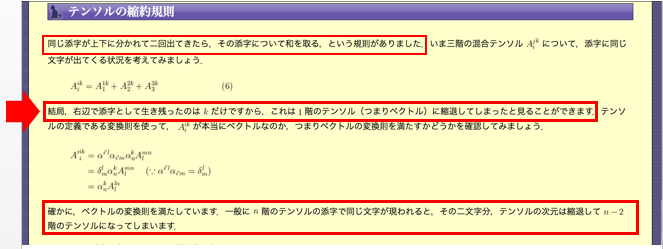
物理のかぎしっぽ「テンソル成分の加法と乗法」を抜粋して転載。なお、赤矢印と赤枠は小野寺による。

物理のかぎしっぽ「テンソル成分の加法と乗法」を抜粋して転載。なお、赤矢印と赤枠は小野寺による。
上記で説明されているように、「上付き添え字」と「下付き添え字」として、同じ文字の「添え字」が表れた場合、その数式は、上付き添え字と下付き添え字に、(3次元時空なら0~2の3個、4次元時空なら0~3の4個の)数字を代入して、各項の和(総和)をとる多項の足し算の数式に展開されます。
そして、展開後はもはや”上下、同じ文字の2つの添え字文字”は存在しなくなります。
このとき、上付き添え字(記号)1つ、下付き添え字(記号)1つの合計2つの添え字(記号)が数式から消えるので、テンソルの階数(次元)が2つ減るという結果が生じます。
このように、”「上付き添え字」と「下付き添え字」で同じ文字の(添え字)ペア1組”ごとに、”次元が2個減る”という現象が起きます。
「上付き添え字」に登場する文字が、「下付き添え字」にも同様に登場する(上付き添え字に登場しない文字は、下付き文字に登場しない)場合は、上・下すべての添え字文字が消えて、次元数ゼロの「スカラー量」になります。
数学上のこの出来事が、物理(学)の世界でもつ意味はなにかというと、スカラー量は、座標変換によって値が変わりませんから、座標不変性が担保されることを意味するということになるわけです。
アインシュタイン方程式(一般相対性理論)は、どのような座標系に依拠している観測者にとっても、方程式の形を変えずに、すべての観測者にとって(そのままの方程式の形で)利用可能です。
観測者が依拠する座標系が互いに等しいか、異なるかにかかわらず、「一般的」に成立しうる物理法則。
それが、「一般」相対性理論です。
何故テンソルなのか?
一般共変性原理(principle of general covariance)は、物理学の法則はすべての座標系で同一の数学的形式を取るべきであることを言っており、一般相対論の発展の中で中心的な原理のひとつである。一般共変性という用語は初期の一般相対論の定式化で使用されたが、現在、微分同相共変性(diffeomorphism covariance)が多く使われる。
微分同相共変性は一般相対論の決定的な特徴ではなく[1]が、議論は現在も残っている。
しかし、一般相対論は(ユークリッド的でない幾何学を使うという)テンソルの言葉で定式化されるという本質的特徴を持つ幾何学であり、物理法則の不変性はこの事実と原理的に結びついている。
(中略)
相対論の深い結論のひとつは、特権を持つ座標系(privileged reference frames)の廃止である。物理現象の記述は、誰が計測するかには依存すべきでなく、つまり、どの座標(標構)も他の座標(標構)と同様であるべきである。特殊相対論は、すべての他の慣性系に優先する特別な慣性系が存在しないことを示しているが、それでも慣性系は非慣性系よりは優遇されている。一般相対論は慣性系の優先性をもなくし、自然を記述する優先された座標系は(慣性系か否かを問わず)存在しないことを示した。
任意の観測者は測定をすることで、その観測者が使っている座標系のみに依存した数値を得ることができる。このことは、(観察者により表現される)座標系には依存せず、独立性をもつような「不変構造」を使い相対性を定式化する方法を示唆している。この不変構造を表すのに最も適切な数学的構造はテンソルであるように思われる。たとえば、加速している電荷により生成される電磁場を計測するとき、その値は使う座標系に依存するが、電磁場自体は座標系からは独立しているとみなされる。この独立性は電磁テンソルにより表現される。
(中略)
不変量
一般相対論の軸となる特徴のひとつとして(座標系による)物理法則の不変性という考え方がある。この不変性はいろいろなやりかたで記述できる、例えば、局所ローレンツ共変(local Lorentz covariance)や一般相対性原理や微分同相共変性(diffeomorphism covariance)。
より明白な記述はテンソルを用いることで可能となる。このテンソル記述による重要な特徴は、(与えられた計量を用いて)階数(ランク)がR のテンソルのすべての添字を縮約すると不変量と呼ばれる数値(スカラー)が得られて、この不変量は縮約に使った座標チャートには無関係になるという事実である。このことは物理的には、(異なる座標系にある)2人の観測者が不変量を求めたときに同じ数値が得られることを意味するので、不変量は観測者とは無関係の意味を持っていることを意味する。一般相対論に於いて重要な不変量としては次のものがある。
- クレッツェマンスカラー(Kretschmann scalar):
相対論での不変量の他の例は、電磁不変量(electromagnetic invariants)や、他にも様々な曲率不変量(curvature invariants)があり、後者には重力エントロピー(gravitational entropy)やワイル曲率仮設(Weyl curvature hypothesis)の研究もある。
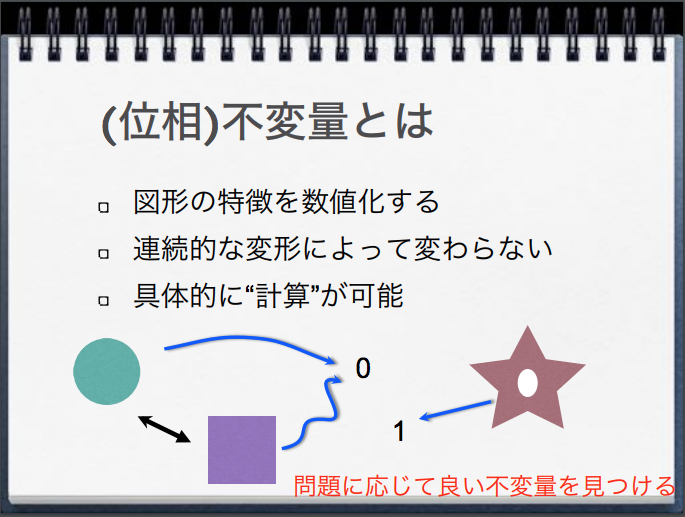
このような一般成立可能な一般相対性理論は、(「リッチ・テンソル」を縮約させることで得られる「スカラー量」である「リッチ・スカラー」などの「座標不変」なスカラー量で構成される方程式です。
リッチ・スカラーは「スカラー曲率」とも呼ばれる。同様にリッチ・テンソルも「テンソル曲率」あるいは「曲率テンソル」と呼ばれることがあるが、後で出てくる「リーマン・テンソル」も同じく「曲率を表すテンソル」であるから、混乱が起こらないように気をつけて使わないといけない。リッチ・スカラーはリッチ・テンソルを縮約して作られている。
リーマン・テンソルを次のように縮約してやって成分を減らしたものを、「リッチ・テンソル」と呼ぶ。

教科書によっては、

と定義するものもあるが、符号は反対になる。
(中略)
リッチ・テンソルを次のように計量を使って縮約してやれば、スカラー量Rが出来上がる。
これを「リッチ・スカラー」あるいは「スカラー曲率」などと呼ぶ。とうとうただの 1 つだけの数値になってしまったが、これは座標の選び方に関係のない、その空間の曲がり具合を表す純粋で代表的な数値だということだろう。この数値の持つ雰囲気はイメージし易い。2 次元曲面に限っての話だが、この値が 0 なら平らな空間であり、数値が大きいほど強い曲がり方をしているという傾向がある。また数値は正負のどちらになることもあり、私の採用した定義の場合には、正なら鞍点のように、負なら球面のように曲がっていることを意味する。しかしこのことは高次元の場合には単純には言えなくなってくるので注意が必要だ。例えばリーマンテンソルに 0 でない成分が含まれているのにスカラー曲率が 0 だということもある。
なお、以下の2つの行列の積をとると、両ベクトル(=反変ベクトルと共変ベクトル)の内積に等しくなります。
内積は、スカラー量で
す。そして、スカラー量は、任意の座標変換に対して不変な値です。
つまり、以下の積をとると、それは、任意の座標変換に対して(座標)不変な値(量)になるのです。
- 「反変ベクトル」に対して定義される座標変換の変換係数(行列)の転置行列
- 「共変ベクトル」に対して定義される座標変換の変換係数(行列)の逆行列
このあたりの事情は、以下のうち、「二つは打ち消し合う」の節の記述文が分かりやすいです。
以下、上記のウェブページより、該当部分を抜粋して転載します。

EMANの物理学 「反変ベクトル・共変ベクトル」より転載。

EMANの物理学 「反変ベクトル・共変ベクトル」より転載。
上記の部分に続く文のあとに、以下の文が現れます。
このような組み合わせでスカラー量を作ることは内積よりも深い意味を持つので特別に「縮約」という呼び方をする。ベクトルがスカラーに縮むというニュアンスである。
なお、計量テンソルについては、先ほどから引用している「EMANの物理学」シリーズの以下の稿がわかりやすいです。
また、
- テンソルの上付添字と下付き添字に同じ文字がペアで出現している場合、その添字を(上下ともに)消去可能で、その結果、テンソルの階数が2つ下がること
と、
- テンソルの添字の縮約記法
との関係については、Wikipedia(日本語版)「テンソルの縮約」に、小野寺がコメントを付した以下を参考にされてください。

Wikipedia(日本語版)「テンソルの縮約」の解説本文。赤文字は小野寺の記入によるもの。
テンソル分解とデータ解析:その他の参考資料
テンソル分解を用いた関係データ分析の事例については、さきに紹介した富士通の他に、以下の解説があります。
- 鹿島 久嗣 「機械学習における関係データのモデル化」
- 鹿島 久嗣 「関係データの機械学習 -行列・テンソル分解によるアプローチ -」
- 林 浩平「テンソル分解による関係データ解析」
- 林 浩平!(NAIST)・石黒 勝彦!(NTT)・ダヌシカ ボレガラ!(東大)「関係データとテンソル分解」
- [スライド] 冨岡 亮太 「行列およびテンソルデータに対する機械学習」(数理助教の会 2011/11/28)
- 納谷 太・澤田 宏 「多次元複合データ分析から時空間多次元集合データ解析技術へ」
- I.Oseledets & A. Cichocki (2017) Tensor networks and deep learning
DTNN: 自然言語処理領域における適用事例
なお、DTNN: Deep Tensor Neural Networksを自然言語処理領域で活用した事例としては、以下があります。冒頭にあげるkoji Maruhashi et.al.論文は、Deep Tensorモデルを構築した富士通研究所に所属する研究者によるものです。
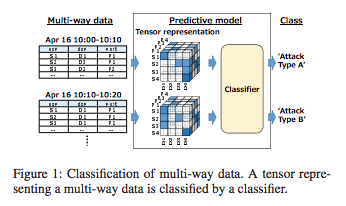
Koji Maruhashiほか, Learning Multi-Way Relations via Tensor Decomposition with Neural Networks, AAAI 2018よりFig.1を転載。
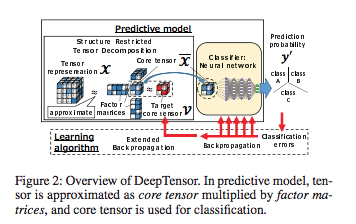
Koji Maruhashiほか, Learning Multi-Way Relations via Tensor Decomposition with Neural Networks, AAAI 2018よりFig.2を転載。
以下は、木構造(Tree-structure)の構文木などのデータを入力値として受けとる多層ニューラル・ネットワークモデルの提案などで著名なRichard Socher教授が名を連ねている論文です。
解説スライドとしては、以下があります。
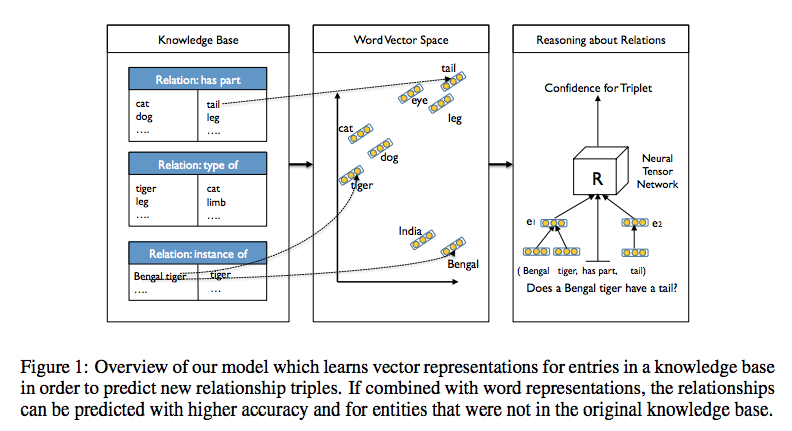
Richard Socher, Reasoning With Neural Tensor Networks for Knowledge Base CompletionよりFig.1を転載。
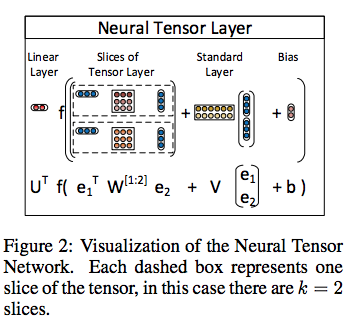
Richard Socher, Reasoning With Neural Tensor Networks for Knowledge Base CompletionよりFig.2を転載。
- Takahiro Ishiharaほか, Neural Tensor Networks with Diagonal Slice Matrices, NAACL-HLT 2018
- Xian Wu et.al., Neural Tensor Factorization, KDD’18
DTNN: 深層ニューラル・ネットワークモデルを情報圧縮する用途での使い方
上記のスライドによると、深層ニューラル・ネットワークモデルとの融合モデルの適用課題としては、以下のようなものもあるようです。
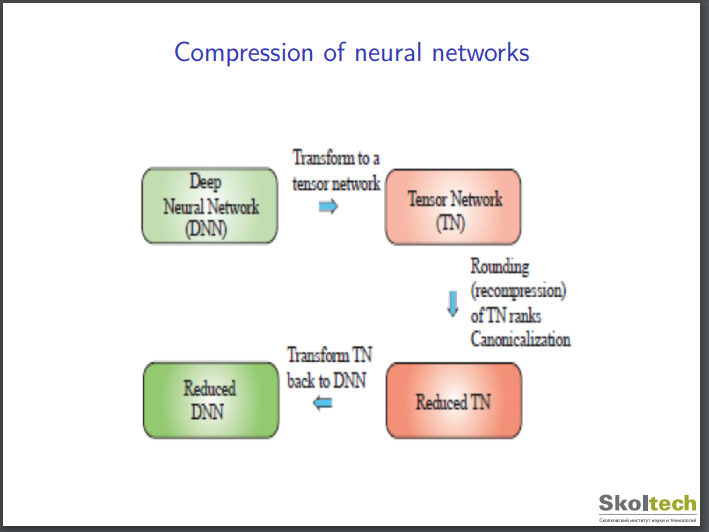
I.Oseledets & A. Cichocki (2017) Tensor networks and deep learningより転載。
これまで、すでに学習済みの深層ニューラル・ネットワークモデルをもとに、そのモデルがもつデータ解析能力(予測能力や分類能力など)を(ほぼ)維持したまま、計算負荷の小さい、より簡素なネットワーク構造(グラフ構造)に変換する方法としては、「蒸留」という方法が知られていました。以下が「蒸留」手法を提案した論文です。
上記の論文を解説した和文の記事とスライドとしては、以下があります。
- DeepX AI Blog (2018/08/28) 「蒸留 第1回」
- Deep Learningにおける知識の蒸留
- WirelessWire News (2016/09/30) 「深層ニューラル・ネットワークの効率を劇的に上げる「蒸留」」
- @nyamu-rd (2018/06/28) 「Deep Leaningのモデル圧縮に関する情報まとめ」
Geoffrey Hinton, Oriol Vinyals & Jeff Dean (2015), Distilling the Knowledge in a Neural Networkは、すでに学習済みの深層ニューラル・ネットワークモデルがもつデータ解析能力(予測能力や分類能力など)を落とさずに、モデルのネットワーク構造(グラフ構造)を、計算負荷の小さい、より簡素な構造に変換するという目的を追求している点では、「蒸留」手法に通じるものがあります。
富士通の技術動向に要注目
この記事では、富士通のDeep Tensorモデルを取り上げました。
富士通は、Deep Tensor以外にも、深層ニューラル・ネットワークの前段に、時系列データの波形図を画像として受け取り、その波形の形状を位相幾何学の知見を用いたデータ解析手法であるTDA(Topological Data Analysis)の解析器を連結させた分析モデルの開発・運用も行っているようです。
- [FUJITSU JOURNAL] 『人々の安心安全な暮らしを支える新しいAI「時系列ディープラーニング」』
- 「トポロジカルデータアナリシスと時系列データ解析への応用」
- [富士通プレス・リリース] (2017年8月28日付)「AI技術により、橋梁内部の損傷度合いの推定に成功」
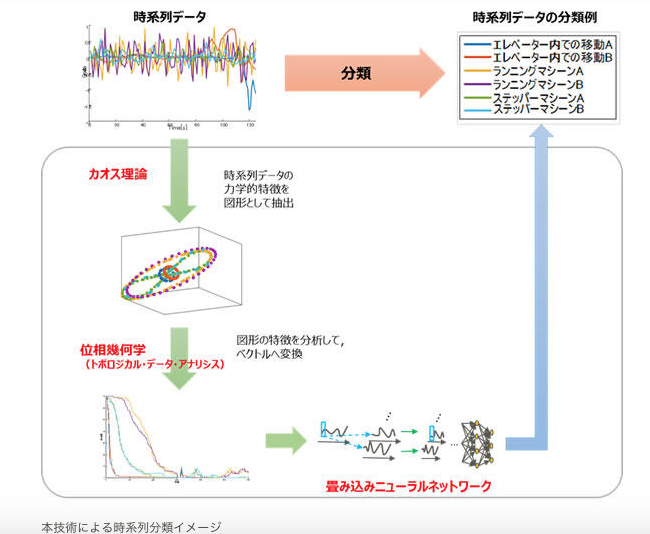
[FUJITSU JOURNAL] 『人々の安心安全な暮らしを支える新しいAI「時系列ディープラーニング」』 より転載。
このため、同社のTDA+深層学習モデルのデータ解析器も、今後、ナノ・テクノロジー領域で利活用がされるシナリオもあるかもしれません。
遺伝情報解析におけるAI技術(3)〜GCNモデル
GCN: Graph Convolutional Networkモデルの登場で、物質の化学結合ネットワークデータを深層学習モデルで取り扱うことができるようになった
グラフ構造のネットワークデータを取り扱うことのできる多層ニューラル・ネットワークモデルであるGraph Convolutional Network手法(GCNモデル)の登場を受けて、ナノ・テクノロジーにおいて、「原子や分子どうしの結合関係」を表したデータを、このGCNモデルを用いて解析する取り組みが現れています。
以下が、その論文の一例です。
上記の論文では、ある特定の分子がもつ原子間の結合構造に焦点を当てることで、ある分子と別の分子が、化学的にみてどれだけ類似した性質(機能)を発揮するのかどうかを推定するmolecular fingerprints(分子レベルの指紋)問題に取り組む上で、GCNモデルを適用しようとしています。
この論文は創薬領域で、意図する薬効・薬能をもつ化学物質の原子結合構造を効率よく探索する課題を念頭においているようです。
論文を執筆したのは5名の研究者のうち、Google社(Google Inc.)の研究者が3名、名を連ねています(残り2人は、スタンフォード大学に所属する研究者)。
なお、Molecular fingerprintsについては、Wikipedia日本語版の項目「分子類似性」の一節を、以下に転載します。
分子構造を、「分子スクリーニング」(構造情報を検索キーとして類似構造を探索する方法)、または、固定サイズ/可変サイズの「分子フィンガープリント」(指紋という特徴によって人物を同定するように、ある特徴を持つ分子を同定する方法)によって表現することで、何百万もの化合物を含むデータベースから類似性に基づくスクリーニングを効果的に行うことができる。分子スクリーニングおよびフィンガープリントは、2次元 (2D) および3次元 (3D) の構造情報をともに含むことができる。
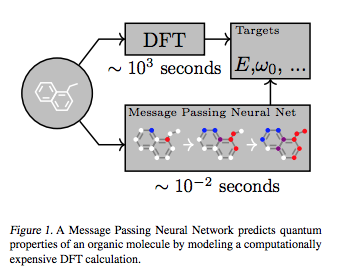
Justin Gilmer et.al., Neural Message Passing for Quantum Chemistry, ICML’17よりFig.1を転載。
また、ナノ・スケール(1mのマイナス9乗のサイズ)の分子レベルや原子レベルの物理空間における挙動を表現する数式である「シュレーディンガー方程式」は、ほとんどの場合、厳密な解析解を数式を解析的に解くことで得ることが困難です。そこで、方程式の近似解を数値計算で推定する場合にも、多層ニューラル・ネットワークモデルが活用され始めています。
[Pythonライブラリ] Chainer Chemistry
深層ニューラル・ネットワークモデルを用いたデータ解析モデルを、Python言語でコード実装する際に用いられるライブラリとして、PFN:Preferred Networks社が無償で提供しているChainerがあります。
そのPFN社から、GCNモデルをChainerにimportすることで、「化学・生物学分野」で「深層学習」モデルを構築することを可能にするためのライブラリがリリースされています。
以下のChainer Chemistryがそれです。
Chainer [1]を使った、化学、生物学分野のための深層学習ライブラリ Chainer Chemistry を公開しました。
- Github page: https://github.com/pfnet-research/chainer-chemistry
- Documentation: https://chainer-chemistry.readthedocs.io
本ライブラリにより、分子構造に対して簡単に深層学習(Deep learning)を適用することができるようになります。
例えば、化合物の分子構造を入力とした毒性の予測や、HOMO(最高被占軌道)レベルの回帰予測など、様々な化学的性質の予測に深層学習を適用することができます。
なお本ライブラリの開発にあたっては、PFN2017夏インターンシップに参加した京都大学の秋田大空さんにも実装に携わっていただきました。
( 中略 )
特長
様々なGraph Convolutional Neural Network のサポート
Graph Convolutional Network (詳しくは下記参照)の登場により、”グラフ構造”を入力として深層学習が適用できるようになりました。Graph Convolutional Networkは現在盛んに研究がおこなわれていますが、本ライブラリでは今年発表されたばかりの論文も含めいくつかのネットワークを追実装しています。
現時点では以下のモデルが実装されています。
- NFP: Neural Fingerprint [2, 3]
- GGNN: Gated-Graph Neural Network [4, 3]
- WeaveNet: Molecular Graph Convolutions [5, 3]
- SchNet: A continuous-filter convolutional Neural Network [6]
データの前処理部分をライブラリ化・研究用データセットのサポート
様々なデータセットを共通のインターフェースで使えるように、ソフトウェアを設計しています。また、研究用によく使用されるデータセットに関してはライブラリ内でダウンロード・前処理を行うことができます。
現時点では以下のデータセットをサポートしています。
- QM9 [7, 8]: 9個までのC、O、N、F原子とH原子から構成された有機分子に対して、B3LYP/6-31GレベルのDFT(密度汎関数法)で算出されたHOMO/LUMOレベル、内部エネルギーなどの物性値をまとめたデータセット
- Tox21 [9]: 12種類のアッセイに対する毒性をまとめたデータセット
学習・推論コードのExample code を提供
ライブラリの使い方がわかるよう、モデルの学習コード・推論コードのExampleも公開しています。すでに実装済みのモデル・データセットに対して手軽に訓練・推論を試してみることができます。
GCN:手法の概要
GCN手法はいかにして、物質の化学結合データを含むネットワーク構造のデータを、深層ニューラル・ネットワークモデル(ディープ・ラーニングモデル)で取り扱うことに道を開いたのでしょうか?
手法のイメージをつかむためには、次の記事が分かりやすいです。
GCNモデルは、多層ニューラル・ネットワークモデルの一種です。
グラフ構造のデータとは?
このモデルは、入力層で入力値として、「グラフ」構造のネットワーク形式のデータを受け取ります。
受け取るデータは、あるノードが他のノードと、エッジ(関係性)で結び合わされた構造を持つデータです。グラフ構造のデータは、ノードとエッジで構成されます。
このグラフ構造のデータについて、上記のtktktks10氏の記事では、ノードを人物(人間)に例えた上で、あるノード(人物)はある特定の(人間)関係のもとで、別の(ひとりあるいは複数人の)ノード(人物)とエッジ(人間関係)で結び合わされている、という例え方をしています。
この例え方では、ノードとエッジはそれぞれ、次のように定義されています。
- ノード:1人の人物
- エッジ:2人の人間の間に成立している人間関係
上記の定義のもと、あるノードAは、他のノードと複数の関係で結ばれています。(人間関係でいうと、職場の上司・部下関係、職場の同僚関係、プライベートの恋人関係、親戚関係、ご近所さんの世帯の関係、など)
そして、「ある人物」に着目した場合、「職場の上司・部下関係」においては、「ある人物」は「Bさん(人物B)」と「Eさん(人物E)」とつながっていて、「プライベートの恋人関係」においては、「ある人物」は「Gさん(人物G)」とつながっています。
グラフ構造データを、多層ニューラル・ネットワークモデルの枠組みのなかで「畳み込む」(Convolution)方式
多層ニューラル・ネットワークモデルでは、入力層で受け取った入力データ(上でみたグラフ構造のデータ)を、入力層に続く(最初の)中間層に受け渡すに際して、入力データ(=グラフ構造のデータ)になんらかの演算処理をかけることで、データから、抽象化された「意味」を抽出します。
従来の畳み込みニューラルネットワーク・モデル(CNN: Convolutional Neural Network)では、入力層で受け取った入力データである画像データに対して、斜めの線だけを浮かび上がらせる(抽出する)フィルタ処理や、画素の明暗の差だけを浮かび上がらせる(輪郭を抽出する)フィルタ処理など、画像がもつ無数の「特徴」のうち、ある1つの「特徴」を抽出することに特化したフィルターを、複数個、用意することで、入力層の次に配置された(1つ目の)中間層に、(斜め斜線や輪郭線など、抽象度の低い)複数の「画像の特徴」を受け渡します。
end-to-endではない多層ニューラル・ネットワークモデル(ディープ・ラーニングモデル)より前の世代の機械学習モデルでは、画像処理フィルターとして、(縦横3画素ずつなどの)局所的な画像領域に対して、どのような画素変換処理を行うフィルターを用意するのかを、人力で設計していました(特徴抽出器の人力設計)。
CNNモデルでは、このフィルター処理を、ランダムな値から、モデルの出力値(推計値)と正解教師用データとの誤差を最小化させる(偏微分演算の連鎖(チェイン)を用いる)誤差逆伝播法アルゴリズムを繰り返すことで、自動的(end-to-end)に作り上げることができることで、人手による介入を要さずに、高精度に画像の分類判定を行う能力をもつ画像判定器を自動的に構築することができるところが、時代を前に勧めました、
GCNモデルにおける「畳込み」は、CNNモデルにおける「畳込み」フィルターとは、仕組みが異なります。
GCNモデルにおける「畳込み」処理とは、単純に以下のイメージになります。
- あるノード(ある人物)に関して、
- ある特定のエッジ(「職場の上司関係」など、なにか1つの関係のみに着目)で結び合わされた他のノード集合(「職場の上司関係」など、なにか1つの人間関係でつながっている人物の集合)
- を「畳み込む」処理
GCNモデルは、最終的にその出力層から、以下のような人間関係図(グラフ構造データ)全体がもつ特徴量を出力します。
- 複数のノード(人物)の間で成立している、複数のエッジ(人間関係)で張り渡された人間関係
GCNモデルは、上記のような「N人(対)N人」の人間関係(自分自身に対する関係を含む)全体の特徴量を抽出するために、以下のような局所的な人間関係
- 「ある特定の人物」を起点として、「ある特定の人間関係」で結ばれた人間集合
を(局所的に)畳み込んでいくデータ処理を、
- 「入力層 -> (1つ目の)中間層」
- 「(1つ目の)中間層 ->(2つ目の)中間層」
- 「(2つ目の)中間層 ->(3つ目の)中間層」
- ・・・
というように、畳み込みの対象となる人間関係の領域の「局所」度合いを、徐々に広げていく(抽象度を高めていく)のです。
それにより、最終的に、人間関係全体の「意味」を抽象的に捉えた「特徴」量を獲得(生成)することを目指す、というのが、GCNモデルが取るアプローチ(データ処理の戦略)になります。
本格的な理解を得るためには、Graph Fourier変換についての数学的な理解が必要になります。
以下、GCNモデルを理解する上でコアとなる部分は、上記のスライドのうち次のスライドになります。
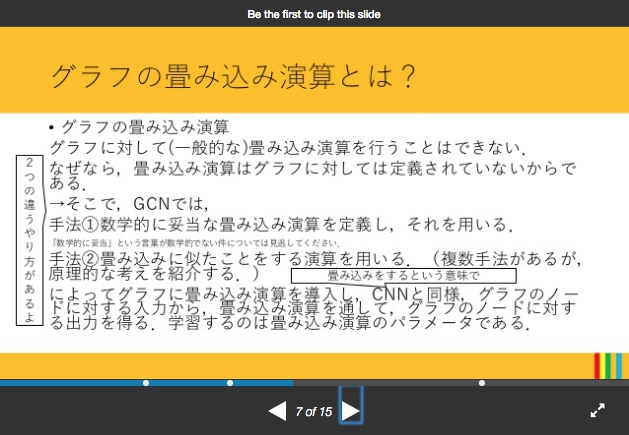
[スライド] KCS Keio Computer Society, Graph Convolutional Network 概説より転載。
GCNモデルの解説記事・解説スライド
- ABEJA Arts Blog (2017年4月27日) 機は熟した!グラフ構造に対するDeep Learning、Graph Convolutionのご紹介
- tktktks10氏 (2018年06月16日)グラフ構造を畳み込む -Graph Convolutional Networks
- [スライド] 東 耕平, [DL Hacks]Graph Convolutional Network LT
- 知識のサラダボウル (2018年5月13日) KerasによるGraph Convolutional Networks 「畳み込みとCNN」
- [スライド] Thomas Kipf, 25 May 2018 (CompBio Seminar, University of Cambridge), Structured deep models: Deep learning on graphs and beyond
このGCNモデルを自然言語解析に適用した際に、どのような結果が得られるのかを掘り下げて解説している論考としては、以下があります。
- piqcy (2018年8月31日付け) Graph Convolutionを自然言語処理に応用する Part1
- piqcy (2018年9月7日付け) Graph Convolutionを自然言語処理に応用する Part2
- piqcy (2018年9月14日付け) Graph Convolutionを自然言語処理に応用する Part3
- piqcy (2018年9月21日付け) Graph Convolutionを自然言語処理に応用する Part4
- piqcy (2018年10月6日付け) Graph Convolutionを自然言語処理に応用する Part5
(関連論文)Graph Attention Network (ICLR 2018)
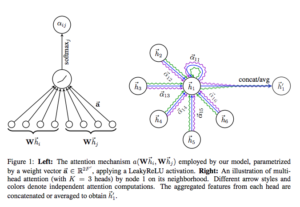
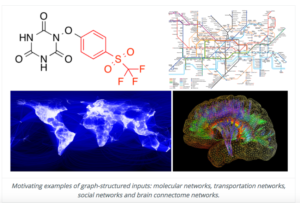
GNC:物質科学以外の領域における適用事例
- Rex Ying et.al., Graph Convolutional Networks for Web-Scale Recommender Systems, ACL’18
- Yaguang Li et.al., Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasrting, ICLR’18
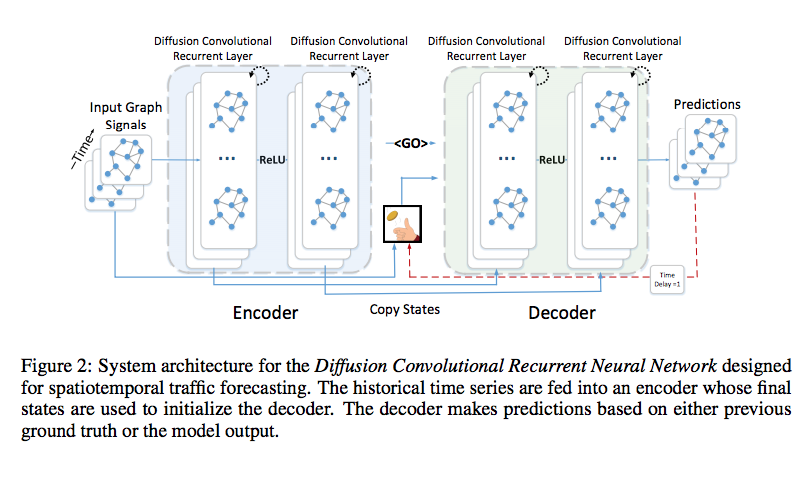
Yaguang Li et.al., Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasrting, ICLR’18 よりFig.2を転載。
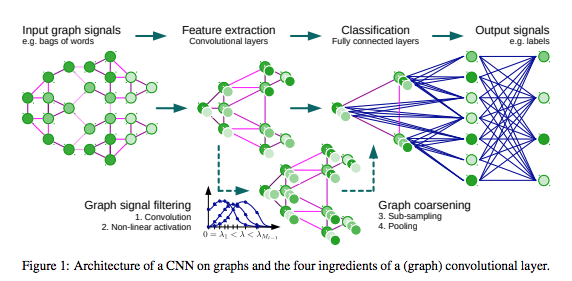
Michaël Defferrard, Xavier Bresson Pierre & Vandergheynst, Convolutional neural networks on graphjs with fast localised spectral filtering, NIPS’16 よりFigure.1を転載。
遺伝情報解析におけるAI技術(4)〜(深層)強化学習モデル
- Marcus Olivecrona, Thomas Blaschke & Hongming Chen (2017), Molecular De-Novo Design through Deep Reinforcement Learning
- Mariya Popova, Olexandr Isayev & Alexander Tropsha, Deep Reinforcement Learning for de-novo Drug Design
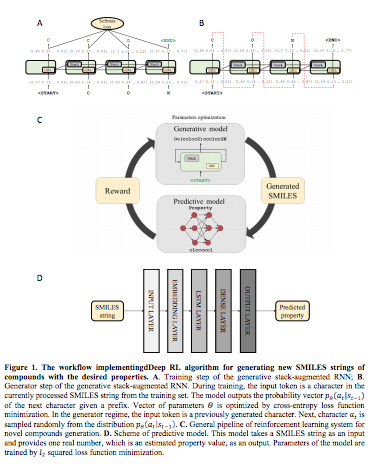
Mariya Popova, Olexandr Isayev & Alexander Tropsha, Deep Reinforcement Learning for de-novo Drug Design より Figure 1を転載。
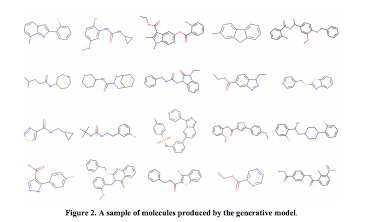
Mariya Popova, Olexandr Isayev & Alexander Tropsha, Deep Reinforcement Learning for de-novo Drug Design より Figure 2を転載。
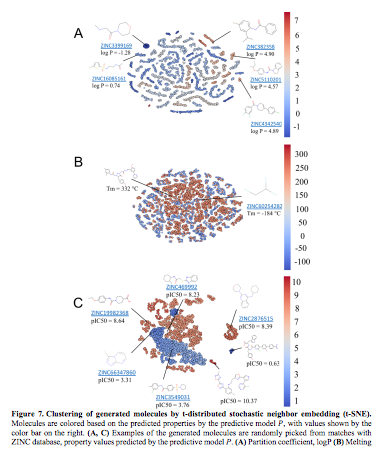
Mariya Popova, Olexandr Isayev & Alexander Tropsha, Deep Reinforcement Learning for de-novo Drug Design より Figure 7を転載。
遺伝情報解析におけるAI技術(5)〜 DNC + GANモデル
DNCモデルとチューリング・マシン
エニグマ暗号機の解読プロジェクト他に参画した英国の数学者・アラン・チューリング氏は、今日の計算機(コンピュータ)の動作原理を概念として、歴史上、初めて考案したという評価が定まっています。
無限に続く記録テープと、テープへの書き込みヘッダと読み込みヘッダで構成されたもの(今日、チューリング・マシンと呼ばれるもの)がそれです。
チューリング・マシンと状態遷移関数などとの関係については、以下のスライド他を参照してください。
このチューリング・マシンを、構造面(機構面)でも、機能面でも模した深層ニューラル・ネットワークモデルとして、Google DeepMind社が公開し、Nature誌に掲載されたDifferential Neural Computerモデルが知られています。以下が、このモデルを提案した論文です。
このモデルは、多層ニューラル・ネットワークモデル(DNNモデル)に、外部記憶メモリを接続(結合)させた上で、ある時点で、外部記憶モデルにどの番地にどのデータを書き込んだり・上書きし、どの番地からデータを読み出すのかを、controller(制御部)と呼ばれるDNNモデルから指示を出す仕組みです。
時系列DNNモデルとして知られるRNNやLSTMモデルも、セルの内部に時系列データの特徴を格納した中間ベクトルを保存していますが、誤差逆伝播法で重みの値が修正されるときに、すべての中間ベクトルの(重みの)数値が一斉に上書きされてしまいます。
これに対して、DNCモデルでは、チューリング・マシンと同様に、メモリ内にデータを書き込んだり、すでに記録されている数値データを上書き変更する際に、書き込み・上書き変更を行うべき特定の(限られた)番地のデータにのみ、アクセスをすることができます。
このような仕組みを備えたDNCモデルは、外部記憶メモリを持たないこれまでのDNNモデルに比べて、より複雑な課題(タスク)を効率よく、精度よく解決する解法を自律的に学習し、推論(探索)する能力を潜在的に秘めているものと期待されています。
DNCの解説記事
- deaikei氏 (2017年03月28日) 外部メモリー付きのニューラルネット”Differentiable Neural Computing (DNC)”について解説するよ
- [解説スライド] 森山 直人氏 Differentiable neural computers
- [解説スライド] Tusuke Iwasawa, [DL輪読会] Hybrid computing using a neural network with dynamic external memory
DNCの発展モデル
DNCモデルを提唱したさきほどのNature所収の論文を引用している論文の本数は、2019年1月13日現在で、Google Scholarによると476本あります。
Alex Graves et.al., Hybrid computing using a neural network dynamic external memory, Natureを引用している論文の一覧(Google Scholarによる集計結果)
これらの後続の論文では、DNCモデルをさまざまな問題意識のもと、それぞれの方面でパフォーマンスを改善させたり、欠点を克服させる試みが提案されています。以下はその一例です。
- Robert Csordas & Jurgen Schmidhuber, Improved Addressing in the Differentiable Neural Computer, NIPS’18
- Improving Differentiable Neural Computers through memory masking, de-allocation and distribution sharpness control
このなかで、Differential Neural TuringモデルとGAN(Generative Adversarial Network)モデルを結合させたモデルによって、分子レベルでみた最適な物質の化学結合構造を推定する課題に取り組んでいる論文があります。以下がそれです。
この論文は、ResearchGateの論文アーカイブ・ウェブページからPDFファイル形式でダウンロードすることができます。
- https://www.researchgate.net/publication/323968939_Adversarial_Threshold_Neural_Computer_for_Molecular_De_Novo_Design
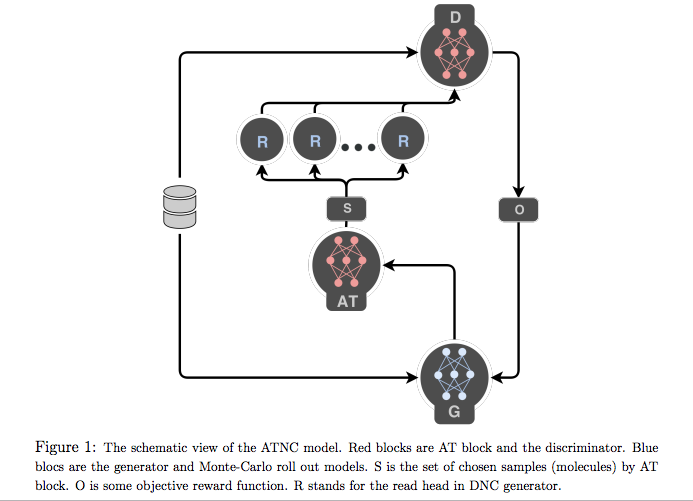
-
- Evgeny Putimn et.al., Adversarial Threshold Neural Computer for Molecular De Novo Design よりFigure 1を転載。
この論文を解説した英文の資料としては、以下があります。
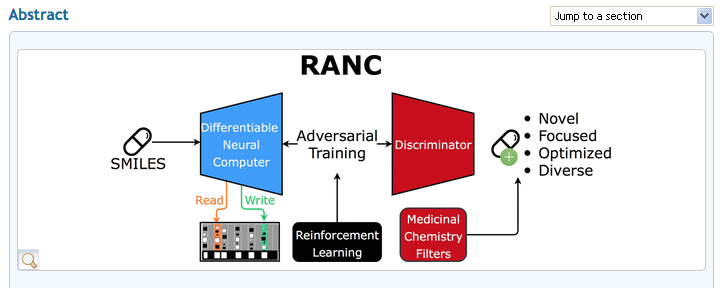
Absrtact
In silico modeling is a crucial milestone in modern drug design and development. Although computer-aided approaches in this field are well-studied, the application of deep learning methods in this research area is at the beginning.
In this work, we present an original deep neural network (DNN) architecture named RANC (Reinforced Adversarial Neural Computer) for the de novodesign of novel small-molecule organic structures based on the generative adversarial network (GAN) paradigm and reinforcement learning (RL).
As a generator RANC uses a differentiable neural computer (DNC), a category of neural networks, with increased generation capabilities due to the addition of an explicit memory bank, which can mitigate common problems found in adversarial settings.
The comparative results have shown that RANC trained on the SMILES string representation of the molecules outperforms its first DNN-based counterpart ORGANIC by several metrics relevant to drug discovery: the number of unique structures, passing medicinal chemistry filters (MCFs), Muegge criteria, and high QED scores. RANC is able to generate structures that match the distributions of the key chemical features/descriptors (e.g., MW, logP, TPSA) and lengths of the SMILES strings in the training data set.
Therefore, RANC can be reasonably regarded as a promising starting point to develop novel molecules with activity against different biological targets or pathways. In addition, this approach allows scientists to save time and covers a broad chemical space populated with novel and diverse compounds.