本記事は、企業が行った研究を学会のように発表議論する場として開催されたCCSE2019のセッション「数学 × Tech」のイベントレポートです。
当該セッションにはZOZOテクノロジーズの渡邊陽介氏、ヤフーの日暮立氏、九州大学の吉田明広氏が登壇され、AI・機械学習の活用が広がっている中で、機械学習への数学的アプローチや、同じタスクを解いているときに数学がどのようにに生きるか、深層学習の強い面と弱い面、数学の強い面と弱い面を強調し、どういったプロダクトができるのかといったことについて話されました。

University of Hawaiiで助教をし転職をきっかけに2018年日本帰国。現在は株式会社ZOZOテクノロジーズと九州大学マス・フォア・インダストリ研究所、訪問研究員などとして機械学習やデータサイエンスの研究に従事。
2009年にエンジニアとしてヤフー株式会社に入社。インターネット広告システムの開発と運用に従事。2016年より、Yahoo! JAPAN研究所にて研究所技術のサービス化推進エンジニアとして従事。
九州大学大学院数理学府修士課程(2年)、マス・フォア・インダストリ研究所 藤澤研究室所属。最適化理論、グラフ理論、深層学習及びそれらの産業応用を専門分野とし、研究を進めている。
目次
深層学習と数理計画問題
機械学習や深層学習の技術が画像認識を筆頭に様々な問題のアプローチとして用いられていますが、そうではない数学的アプローチとして数理計画問題を用いた実問題の解決について吉田氏は以下のように始めました。
吉田氏:機械学習をよくやっている方は、無意識に実際の問題を深層学習の問題に起こして、何かしらに即した結果をフィードバックすることによって、レコメンドに使ったりなどしていると思います。
しかし、深層学習では対応しにくい問題に対して、数理計画問題を用いたアプローチについてお話しします。
そのための題材として、今回は席替え問題について考えてみようと思います。

席替え問題へのアプローチ
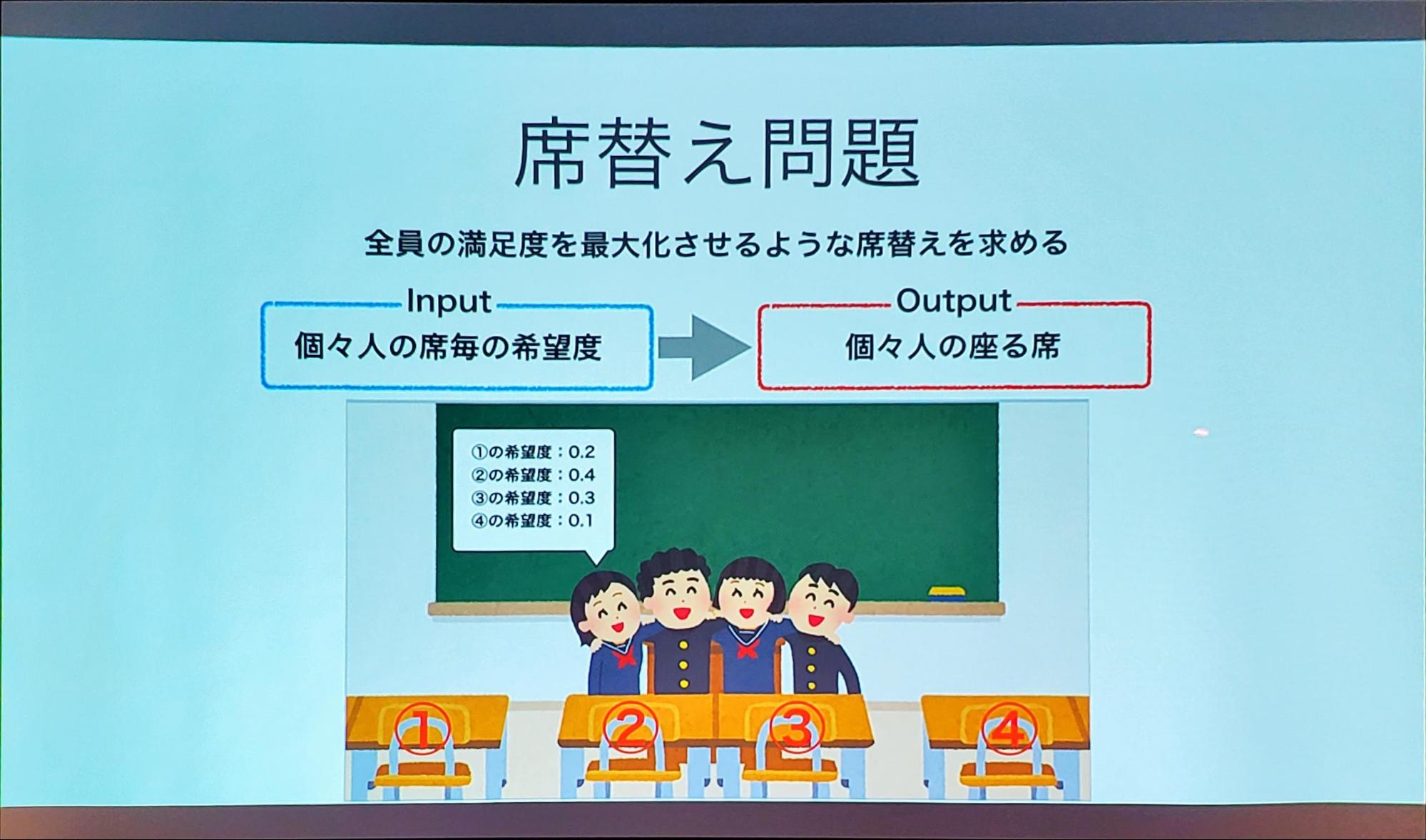
席替え問題では、クラスの席替えを考えたとき、みんなの希望を満たせるような席替えを考える問題です。
生徒と席が同じ数だけあり、各生徒が各席に持っている席の希望をできるだけ満たす(希望度の最大化)ような席替えを求めなければなりません。
問題のインプットには一人ひとりの席の希望度とし、結果となるアウトプットには誰がどこに座るかの席替え結果を出力します。
ニューラルネットワークによるアプローチと問題点
この問題をニューラルネットワークによって求める場合には、以下のようなことが問題になってしまいます。
- ブラックボックス化
- 非現実な答えを出力する危険性
- 大量のデータが必要(+正解ラベルを作るコスト)
吉田氏:例えば、MNISTは画像をインプットとしてアウトプットに数字の予測結果が出てきます。出力確率が最も高いクラスを予測の結果とします。このようなアーキテクチャを今回の問題に適用しようとすると、インプットのレイヤーに生徒の希望度を入れて、アウトプットとして座る席の確率を返すというモデルが考えられます。
このとき大きく分けて三つの問題が考えられます。
1つ目がブラックボックス化という問題で、このニューラルネットワークによって解いた問題について、本当に全員の希望度を満足している保証がありません。つまり最適性の保証がありません。
二つ目に非現実な解を出力する危険性があります。例えば女の子(下図参照)の座る席が3番席の予測になったとします。そして、別の男の子の座る席を3番と予測してしまった場合、3番の席に二人が座れている状況になってしまいます。これは実際にはあり得ない状況なので防がなければなりません。
最後の三つ目は、大量のデータが必要になってしまう問題があります。大量の席替えと大量の席替え結果のデータを用意する必要があります。
渡邊:このブラックボックスは俗に言う、ニューラルネットワークの精度がよくても、その精度が理論的に担保できない、つまり上手くいってても何故上手くいっているのかがわからない、という事ですね。
データに関して言うと、MNISTが数万枚必要で、今回は席替えラベルをどう作るのか、また、たくさんのデータがこの問題をニューラルネットワークで解こうとすると必要になってしまいますね。

MNISTは0~9のどれかの答えはわかっていますが、席替え問題ではクラスの人数が変わってしまった場合には、そのままのニューラルネットワークのアーキテクチャが対応できなくなってしまいます。
こういった場合には数理計画問題を起こすことでアプローチすることができます。
数理計画問題によるアプローチ
※ここからは数式が出てきますが、完全に理解する必要はありません。
数理計画問題とは(引用 : 株式会社NTTデータ数理システム 数理計画問題とは)
数理計画問題とは,「与えられた条件の下で,望ましさの尺度を表す何らかの関数の最小値(最大値)を求め,さらにその最小値(最大値)を与える不特定要素の値を決定する」という問題です.
上記における,「与えられた条件」は制約条件,「望ましさの尺度を表す関数」は目的関数,「不特定要素」は変数と一般に呼ばれています.この用語を用いて書き直すと,数理計画問題とは,「制約条件を満たす範囲における目的関数の最小値(最大値)及びその最小値(最大値)を与える変数を求める問題」といえます.
例えば,x >= 0において3x+2の最小値を求める問題は,数理計画問題です.この場合,制約条件はx>=0,目的関数は3x+2,変数はxとなります.
この問題は数理計画の世界では次のように書かれます:
- 目的関数:3x+2→最小化
- 制約条件:x>=0
考える間もなく,上記の数理計画問題の最もよい目的関数値は2(x=0のとき)となります.このときの変数の値を最適解と呼びます.
最適解を求めることを「数理計画問題を解く」あるいは「最適化する」といいます.

今回は席替え問題を0-1整数計画問題の形に定式化しています。
インプットに生徒の希望度ベクトル(各生徒が各席に持っている座りたさ)として、目的変数には着席ベクトルとして、生徒が座っていなければ0、生徒が座っていれば1を立てます。
吉田氏:例えばスライドにある女の子(下図参照)の満足度をどう計算するか説明すると、この子(生徒i)が②の席に座ったときにはxi2にだけ1が立つことになり、0.4×1=0.4でそれ以外は全て0になり、席に対しての和をとって0.4が求まります。
これを生徒全員についての和を取ったものが目的関数になり、この最大化を目指します。

次に、1つの席に2人の生徒が座っている状態など現実的でない結果を防ぐために制約条件を決めていきます。
今回は、以下の三つを制約式としています。
- 1つの席に1人しか着席できない
- 1人1つの席しか着席できない
- 席には着席するかしないかの2択

これで、数理計画問題を解くための目的関数と制約条件を定式化することができました。
手計算でも問題を解くことは可能ですが、数理計画問題を解く手法についてはこれまで研究されてきており、そのアルゴリズムを実装されたソフトウェアのソルバーによって問題を解くことができます。
数理計画ソフトに標準的に搭載され、エクセルにもソルバーは搭載されています。

ニューラルネットワークの課題として、柔軟性の無さが挙げられましたが、これについて数理計画問題は柔軟性があります。
先ほどまでの結果を求めたあと、例えばある生徒と生徒の席がとなり同士になることを防ぎたいとします。このとき数理計画問題では、制約条件を追加して再度ソルバーで計算するだけで、条件を満たした結果を得ることが可能です。

ここまで、席替え問題として数理計画問題を解いてきました。
数理計画問題は、ニューラルネットワークに比べて最適性が保証されることや、現実的に実行可能な制約を考えることができるという強力な武器を持ってますが、もちろんデメリットもあります。
必要なのは、双方をメリットとデメリットを理解し、適切な方法で問題にアプローチすることです。
以下はニューラルネットワークと数理計画問題のメリット・デメリットをまとめたものです。
- ニューラルネットワーク
- メリット
- 特徴量の自動抽出
- タスクによっては人間よりも高精度
- デメリット
- ブラックスボックス
- 考慮しづらい制約が存在
- メリット
- 数理計画問題
- メリット
- 最適性の保証
- 現実に実行可能な制約を考慮可能
- デメリット
- 問題毎に最適性を求めるので1つの最適化の結果を別の問題に転用できない
- (深層学習より)ユーザが少ない(※個人の感想)
- メリット
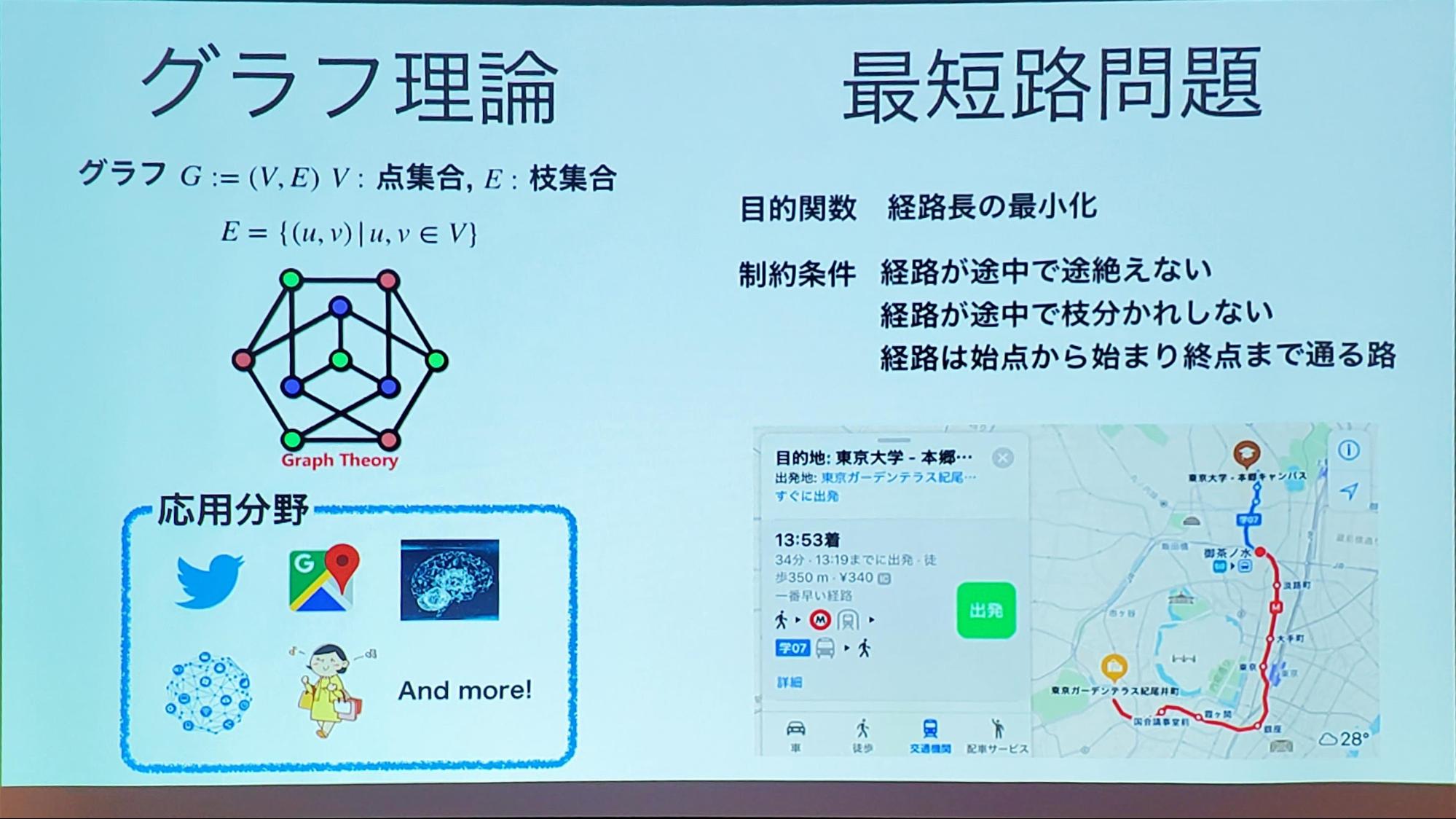
グラフ理論・数理計画問題を用いた実問題へのアプローチ
バイクシェアリング
日暮氏は、「バイクシェアリングにおける再配置問題」について、ヤフーと九州大学の共同研究として取り組んでいます。

日暮:ユーザが駐輪場に行き、借りたい自転車が無いような状態や、逆に自転車を借りて目的の駅まで行ったときに止めることができる駐輪場が無いような場合を防ぐために、いついかなる時に行ってもある程度自転車を止める場所があるように自転車の数を常にうまく調節することが必要です。
バイクシェアリングにおける再配置問題では、この問題をグラフ構造を用いて最適化問題を解いています。この問題では、各駐輪場の利用者数を深層学習によって事前に予測しています。そして、予測した需要から各駐輪場に必要な自転車台数と自転車を再配置するトラックの最適なルートを数理計画問題によって求めるようなアプローチをとっています。

数理計画問題を用いた実例
バイクシェアリングの再配置問題のように、深層学習と数理計画問題を組み合わせることでさらなる問題解決へのアプローチが可能となります。
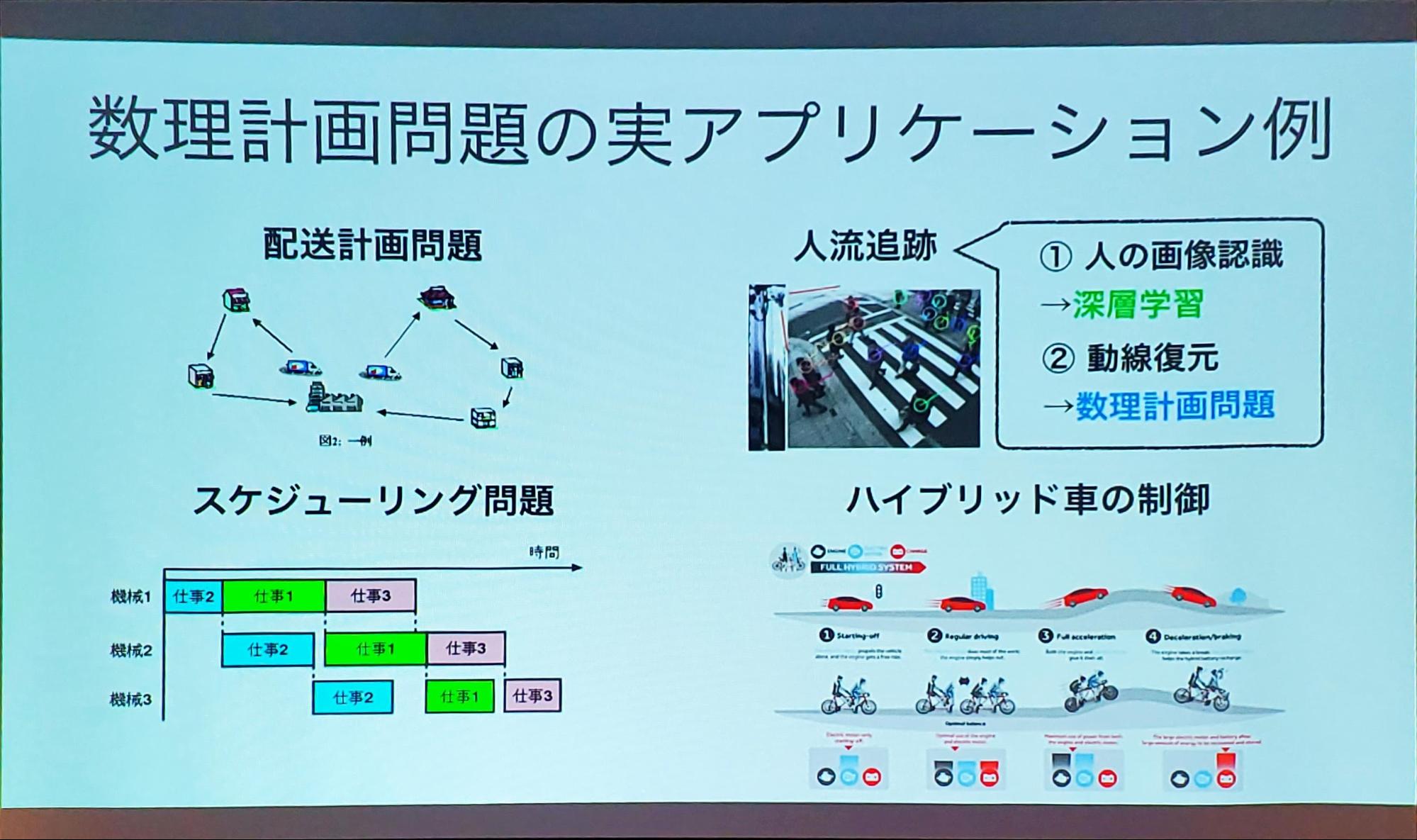
人流追跡での動線復元
画像認識でも数理計画問題を取り入れることによって、例えば、人流追跡の問題であるディテクションが切れてしまう問題を解決することができます。
吉田:画像認識による人流追跡をしようとしたときに、人と人が重なった時などに検知ができなくなってしまうことや人のIDが入れ替わってしまうことがあります。そのとき人の動線を復元するために数理計画問題を解いています。
渡邊:顔認証でも認識にバウンディングボックスがありますが、顔と何かが重なった瞬間に切れてしまうことがあります。その動線の復元に数理計画問題を解くことで解決しているというわけですね。
ハイブリッド車の制御
ハイブリッド車を開発する際にも、数理最適化を解くことでアプローチできる問題があります。
吉田:ハイブリッド車を開発するとき、モーターとエンジンをどのような形で組み合わせれば最適化であるかという問題があります。
あるモーターとエンジンの組み合わせはどれくらいのエネルギー効率を持っているのかを見たいときに、テストコースで1時間の走行、30分くらいの走行によって測ることができます。
そのテストコースを最も効率的に走る時の制御の仕方を求める問題を解いています。
この問題を解くときは、車の状態量を離散化し、短い30秒くらいごとの走行のさせかたを学習させます。この車を30分間走らせたときに、一番燃料消費量が最小になるような走り方を求める問題をグラフ理論を用いた制約付き最短路問題に落として解いています。
質疑
質疑時間では、数理計画問題のメリットである”最適性の保証”は、事前の深層学習によって担保されなくなる可能性について質問が出ました。
質問:深層学習と数理計画問題を組み合わせたときに、数理計画問題を解いたときに最適性が保証されますが、事前の深層学習は間違えてしまうことあると思います。例えば、先ほどの需要予測の例で、そこが最初にミスることがあれば、その後の最適が最適では無いのかなと思います。
吉田:そうですね。深層学習の部分でのミスを考慮して、今回のバイクシェアリングにおける研究では数理計画問題を定式化するときに少し緩めの仮定を入れています。バイクシェアリングの例では、需要予測で完璧な台数のイン・アウトが求まっていないとき、予測ができてなかったとしても、この駐輪場が比較的入って来やすいポートか出て行きやすいポートなのか、ポートの特徴だけを予測できているというもとで最適化問題を解いています。
つまり、需要予測に多少は歪みがあったときはその需要予測に基づいて最適解を求めてしまうので、確かに多少ずれてしまうことがあります。
おわりに
今回のセッションでは、昨今の機械学習ブームによって様々な問題解決にこれらの技術が使われていますが、数学的アプローチでも解決できる問題は多いと渡邊氏は指摘し、以下のよう締めくくりました。
渡邊:今回お伝えしたかったメッセージは、全てを深層学習ですることもいいかも知れないですが、ある部分を深層学習でやって、他を最適化でやることによって、実応用で安心するという点があります、医療や自動運転への深層学習は中身のアルゴリズムが全てブラックボックスでは困る訳です。また、グラフ理論の最短経路問題とかは深層学習でやる問題では無いですし、数学でやった方が良いですよね。お互いの良い点悪い点を洗い出して、組み合わせることによってプロダクトとして使いやすくなると思います。数学のテックへの様々な応用の仕方を分かっていただけたら、嬉しい限りでございます。