AIのアルゴリズムは常に進歩しており、日々新たな論文やサービスが発表されています。
一方、現在「AI」と呼ばれているようなシステムのなかには、実は古典的なアルゴリズムで動いるものもあります。その多くは昔ながらの統計学的手法に基づいたものです。
本記事では、AIの代表的なアルゴリズムを挙げ、基本的なアルゴリズムの仕組みを紹介します。
目次
AIのアルゴリズムとは
「アルゴリズム(Algorithm)」という言葉を一言で説明するのは困難です。とりわけ、日本語での適切な翻訳もありません。
「アルゴリズム」という言葉が日常的に使われるとき、それは何かの手続きのことを指しています。AIにおけるアルゴリズムもその理解に近く、端的に言えば「計算の手続き」のことを指しています。
アルゴリズムの基本構造
アルゴリズムで最も一般的なものは「ソート」です。例えば、「横に並んでいる数を小さい順に並び変える」という問題を考えてみましょう。

色々な解き方・考え方がありますが、ここでは単純に左から数の大小関係をチェックしていきましょう。
左の数字より右の数字のほうが小さい場合、左右の関係をひっくり返します。そして、右の数字が左の数字よりも大きくなるまで、この作業を繰り返します。
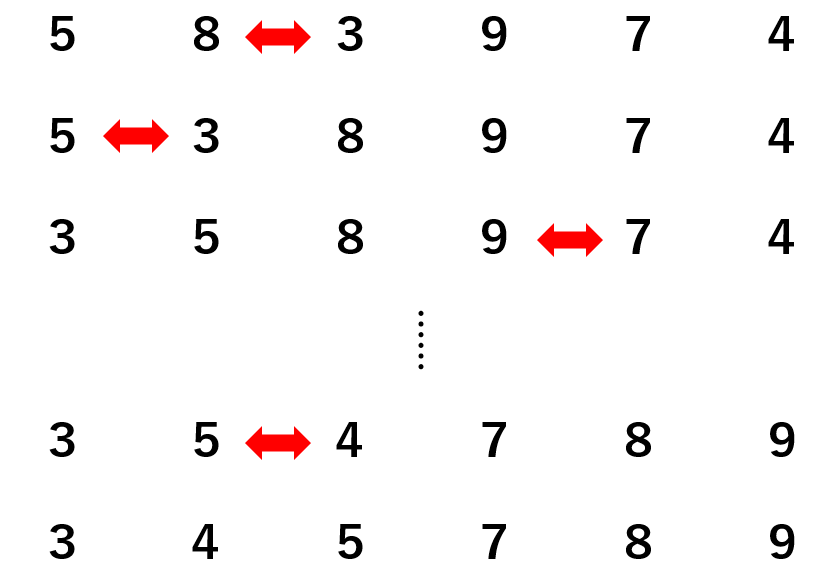
この手続きが、計算の手続きであり、すなわちアルゴリズムです。アルゴリズムのイメージは掴めたでしょうか。
アルゴリズムのメリット
アルゴリズムをプログラミングで実装することで、そのプログラムを使えば誰でもそのアルゴリズムを使うことができます。
AIにおけるアルゴリズムも同様で、私たちはアルゴリズムがどのような仕組みで動いているのか、どのように数学的に設計されているのかを知らなくても、そのアルゴリズムを使うだけで結果が得られます。
というのも、プログラミングで実装されたアルゴリズムは「関数」の形をしています。プログラム上の関数は「入力を出力に変換するもの」です。
私たちは、関数が内部でどのように動いているのかを知らなくても、そのプログラムを使う上ではまったく問題ないのです。
しかし、アルゴリズムがどのように動いているのかを理解することで、AI自体への理解を深めることができます。本記事ではさまざまなアルゴリズムを紹介しますが、直感的に分かりやすくするために、数学的な説明を避けつつ解説していきます。
教師あり学習のアルゴリズム
回帰と分類
教師あり学習の手法は、大きく分けて回帰(regression)と分類(classification)の2つに分けられます。回帰の手法はあるデータの「将来の数値を予測する」問題を取り扱い、分類の手法は、あるデータが「どのクラスに属すのかを予測する」問題を取り扱います。
別の言い方をすれば、回帰の手法は「連続値」を扱い、それに対して分類の手法は「離散値(非連続な値)」を扱います。以下の図は回帰と分類の違いを示しています。
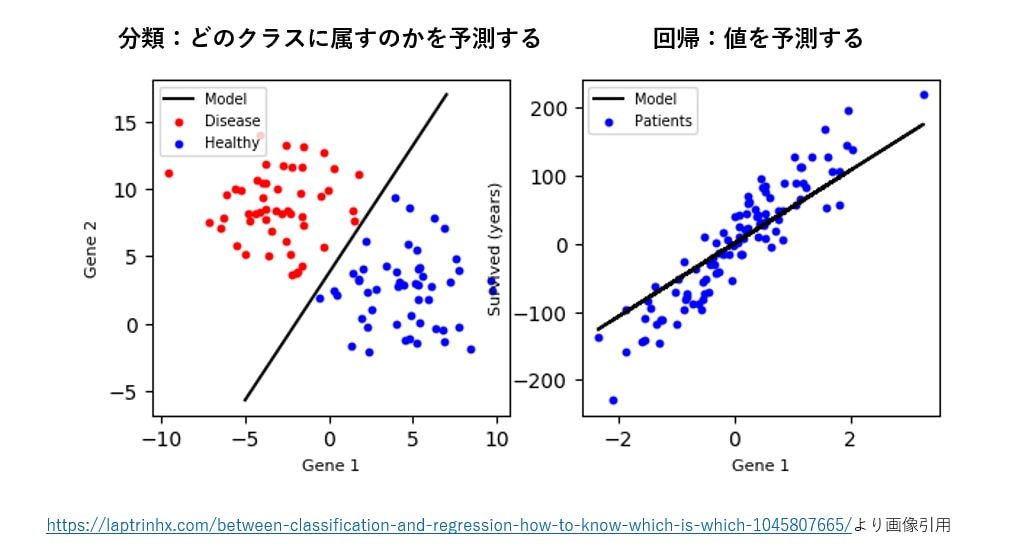
回帰分析
回帰分析は、予測したい目的変数を他のさまざまな説明変数に基づいて予測します。
説明変数が1つの場合、単回帰分析と言います。目的変数yを従属変数、説明変数xを独立変数に解釈すると、単回帰分析はaとbをパラメータとして持つ「y=ax+b」という形の一次関数で表現できます。また、説明変数が複数の場合は重回帰分析と言います。
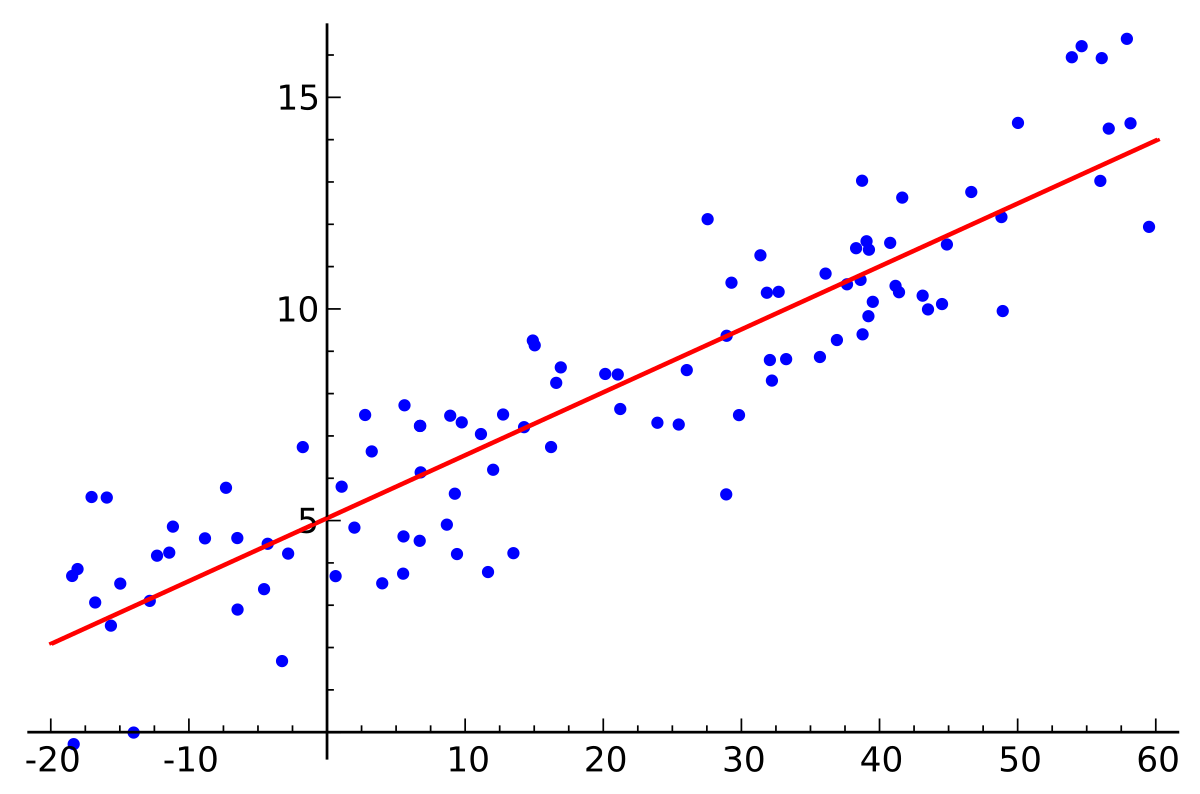
出典:https://en.wikipedia.org/wiki/Linear_regression
回帰分析には「線形回帰」と「非線形回帰」の区別があります。やや厳密さを欠く直感的な説明ですが、上記の図のような関係、言い換えればデータ間の関係を直線的に表現できるような回帰分析を「線形回帰」と言います。
k最近傍法
典型的な分類問題のアルゴリズムは、「k最近傍法」です。座標上に散らばっているクラス分けされたデータ群に対して、未知データがどのクラスに属すのかを判別します。
未知データから距離が近い順にk個データを取り出し、そのk個のデータのなかで最も数が多いクラスに未知データを振り分けます。図にすると以下のようになります。

既にラベルが貼られたデータ群に対して、未知データがどのクラスに属すのかを判別します。この例では、赤丸のクラス、青星のクラス、緑ダイヤのクラスの3種類があります。
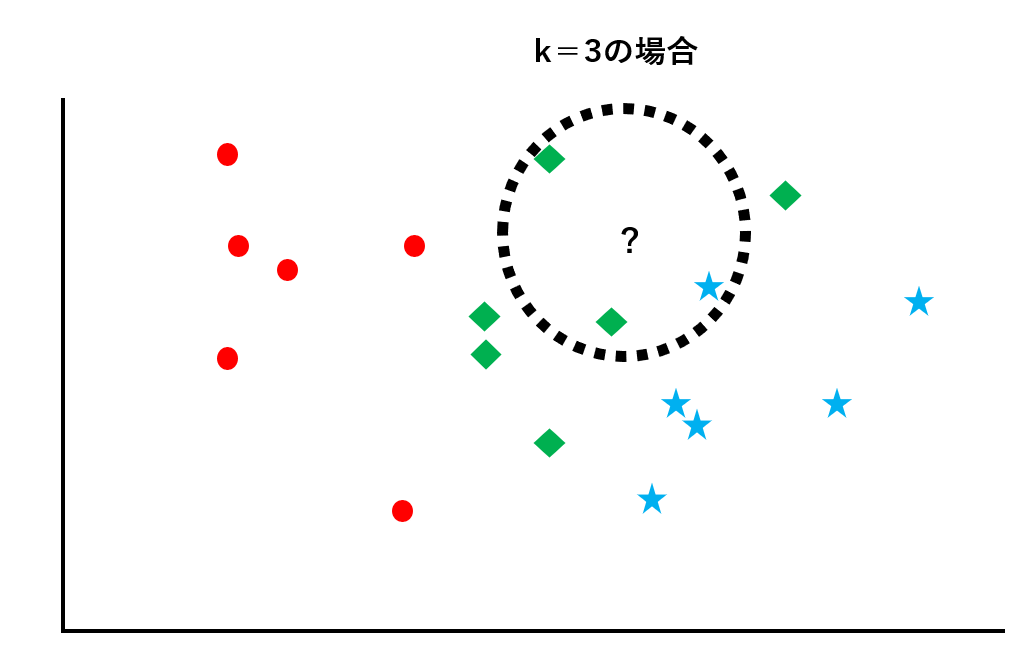
次に、k=3として未知データから距離の近い順に3つのデータを取り出します。この例では青星が1つ、緑ダイヤが2つなので、多数決をとってこの未知データは緑ダイヤのクラスに属すものと判断します。
ランダムフォレスト
ランダムフォレストとは「決定木」というアルゴリズムを複数組み合わせたものです。決定木とは何かは、以下のようにフローチャートで表現するとよく分かりやすいのではないでしょうか。
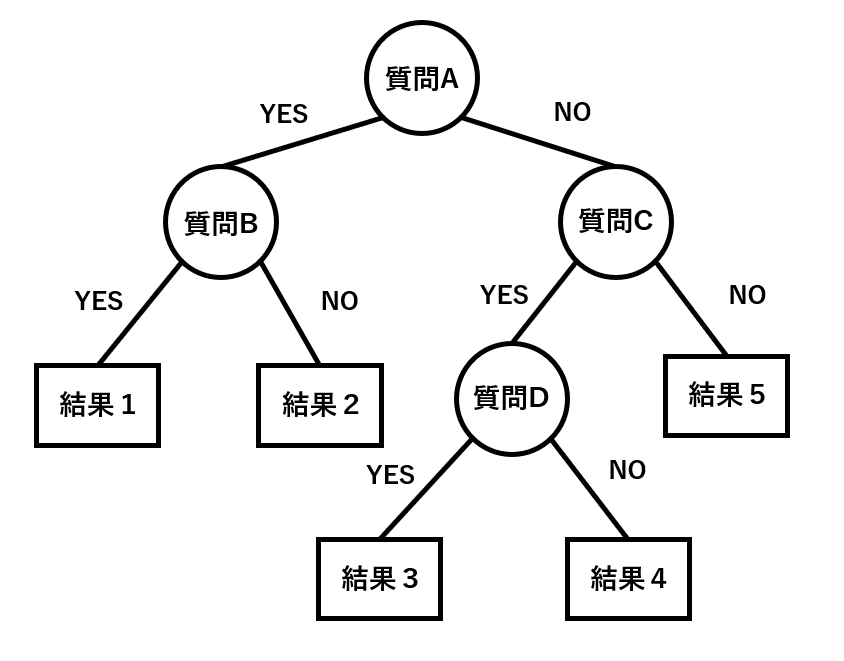
上記の画像は、質問に対してYES/NOで答えていく決定木を表したものです。
ランダムフォレストはこの決定木を複数並べて、その結果を多数決で決めるようなアルゴリズムのことを指します。
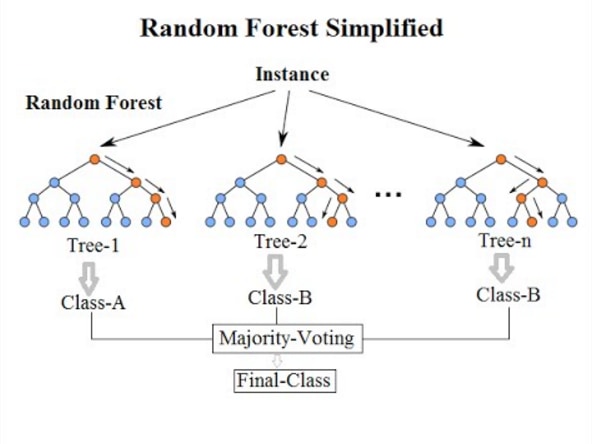
出典:https://community.tibco.com/wiki/random-forest-template-tibco-spotfire
また、決定木には回帰決定木と分類決定木の二種類があるため、ランダムフォレストはどちらの問題にも対応できます。
サポートベクトルマシン
サポートベクトルマシンは、データ群に対して「マージン最大化」という計算をするアルゴリズムです。図を参考にしながらそのプロセスを追っていきましょう。
赤丸と青星が散らばっているデータに対して、両者を「境界線」でわける問題を考えます。しかし、この図の通り、線の引き方はたくさんあります。
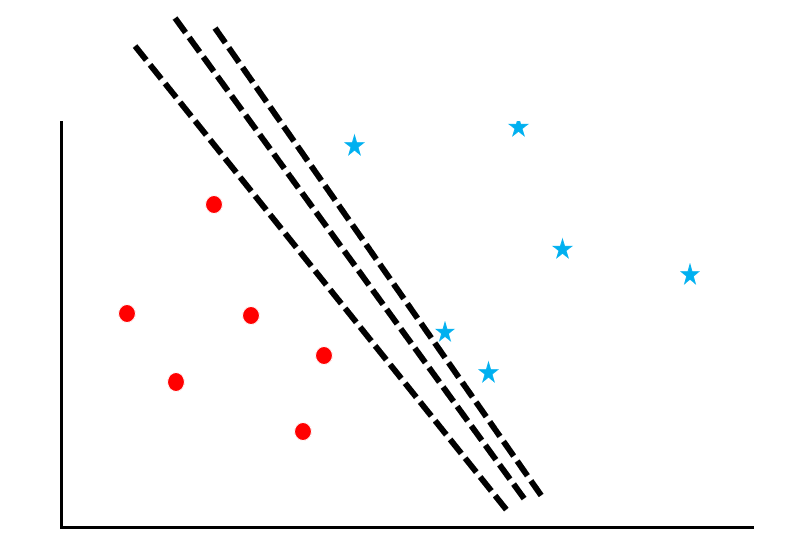
ここで「サポートベクトルのマージンを最大化すること」を考えます。サポートベクトルとは境界線の近くのデータのことを指し、マージンとは境界線とデータとの距離を意味します。図の緑の線がマージンです。
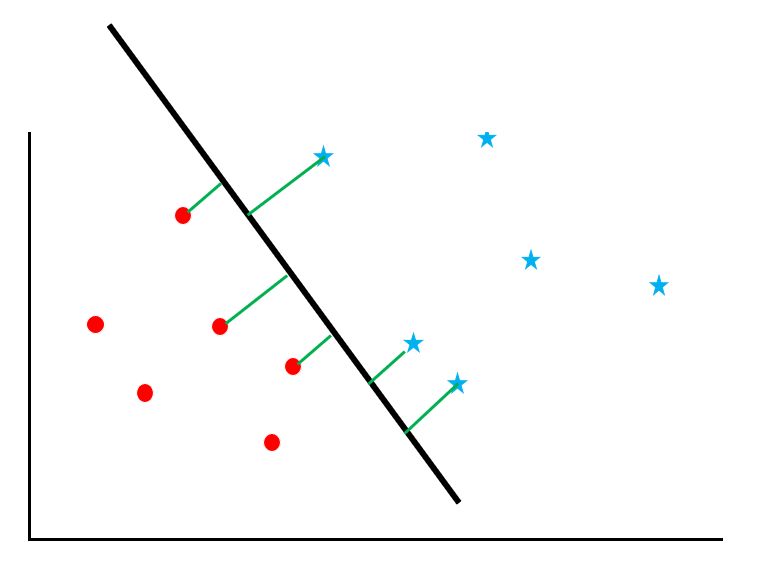
このマージンがもっとも大きくなるような線を境界線とします。こうすることで、「誤判定」を避けることができます。なぜなら、2つのクラスのうち、どちらに属すのかが曖昧なデータが、マージンの最大化によって少なくなるからです。
このサポートベクトルマシンは、回帰問題にも分類問題にも対応できるアルゴリズムです。
教師なし学習のアルゴリズム
クラスタリング
代表的な教師なし学習のアルゴリズムは、「クラスタリング」です。
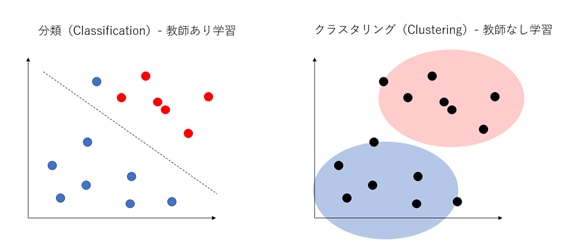
クラスタリングは未知データをグルーピングしていくアルゴリズムです。いわゆる分類(教師あり学習)のアルゴリズムとの違いは、以下の図のように表すことができます。
k-means法
k-means法は、最もよく用いられるクラスタリングのアルゴリズムです。
まず、散らばったデータ群に対して、ランダムにk個の重心点を定め、これを核とします。
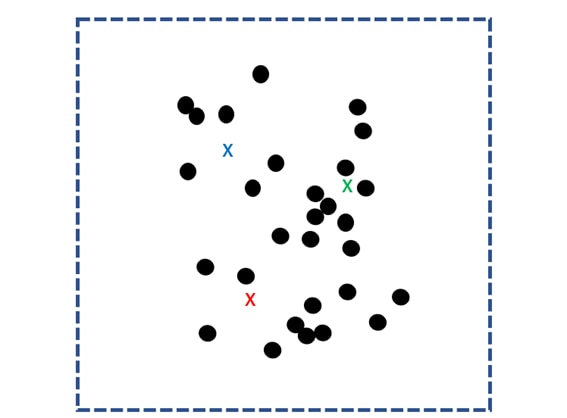
そして、k個の核との距離をすべてのデータに関して計算し、最も近い核のグループにわけます。このグループのことを「クラスタ」と言います。
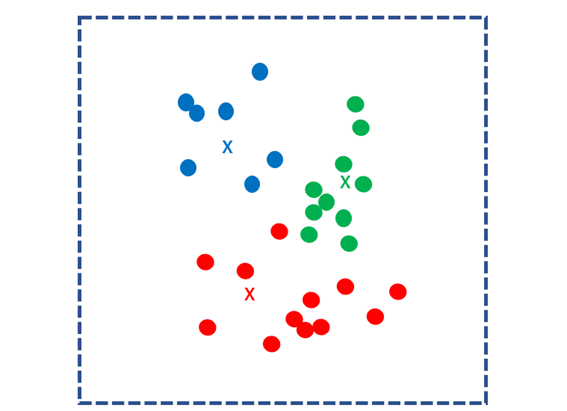
次に、クラスタごとの重心点を求め、それを新たなk個の核とします。同様のプロセスを繰り返し、各データを最も近い重心点のクラスタにわけます。
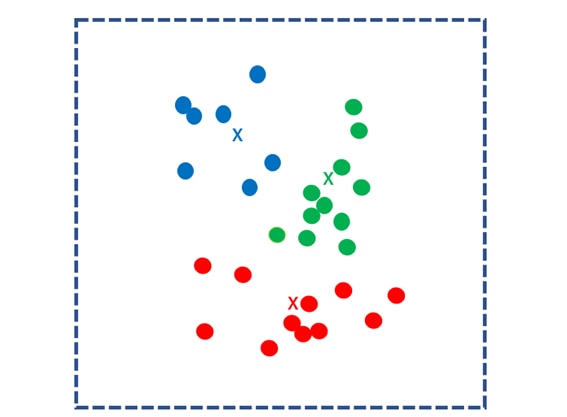
このプロセスを重心点が移動しなくなるまで繰り返します。重心点が更新されなくなったとき、計算は終了です。
強化学習のアルゴリズム
Q学習
Q学習とは、「Q値を学習するアルゴリズム」のことです。Q学習を学ぶうえで避けて通れないのが数式の理解なのですが、ここではできるかぎり単純化して解釈します。
Q学習は以下のような数式で表現できます。
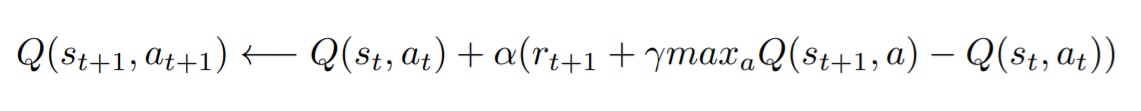
このアルゴリズムは「状態sにおいて、報酬rを最大化するような行動aを選択する」と解釈することができます。
その行動を取ることで得ることのできる報酬の期待値をQ値とあらわします。過去の行動の価値が積み上がった結果として現状態sが出来ているので、現状態sは常にQ値を持っています。そして、次にどういう行動を取るかによってQ値を更新していくことができます。一番大きいQ値の行動を選択すれば報酬にたどり着ける可能性が上がります。
パラメータはαとγの2種類があります。αは「学習率」で、Q値の更新の急さを定めます。γは「割引率」で、次の行動のQ値をどの程度信頼して現在のQ値に組み入れるかを表します。これを最適化することで、結果的に適正な学習が行われます。
他の強化学習アルゴリズム
他の強化学習アルゴリズムには、モンテカルロ法やSARSAがあります。モンテカルロ法は、かなり古典的なアルゴリズムですが、報酬を求めるプロセスを逐次的に行うことができないため、学習に時間がかかります。
この欠点を克服したのがTD学習と言われる強化学習アルゴリズムで、SARSAはQ学習と同じTD学習に属すアルゴリズムです。
まとめ
この記事では代表的なAIのアルゴリズムについて紹介しました。アルゴリズムを理解することは、AIの仕組みを理解することに繋がります。
ここで紹介したアルゴリズムは、最も基本的なものであり、全体のごく一部に過ぎません。より高度な内容になりますが、最新のAIに興味のある人は最先端のアルゴリズムのトレンドを追いかけてみるのも良いでしょう。
また、興味深いことに、古典的なAIのアルゴリズムのなかには、ディープラーニングの手法と組み合わせることで大きな成果を出しているものもあります。AIの仕組みはまだまだ手探りの段階で、「一筋縄ではいかない」ものだということが分かります。