クラスタリングは、顧客データの分析や商品のレコメンドシステムなど、社会に広く応用されている機械学習手法です。
分類アルゴリズムは、統計学やAIの分野で昔からさまざまなものが考案されてきましたが、クラスタリングはその最も成功した例の一つということができるでしょう。
しかし、読者の中にはクラスタリングについて詳しく知らない方もいるのではないでしょうか。
そこで今回は、機械学習の代表的な手法の一つである「クラスタリング」についての概要やメリット・デメリット、活用事例まで詳しく解説していきます。
| 【この記事でわかること】※クリックすると見出しにジャンプします |
▼機械学習について詳しく知らない方は、こちらの記事がおすすめです。
目次 [非表示]
クラスタリング(Clustering)とは
クラスタリングとは、「データ同士の類似性によってデータをグループごとに分ける機械学習の手法」です。
その分類された各部分集合のことを「クラスタ」と言います。クラスタリングはクラスタ分析やクラスタ解析と呼ばれることもあります。
クラスタリングは、機械学習の手法の中でも「教師なし学習」に分類されます。各データに特徴を付与(ラベリング)する必要がないため、大量のビッグデータを自動で分類することが可能です。
分類との違い
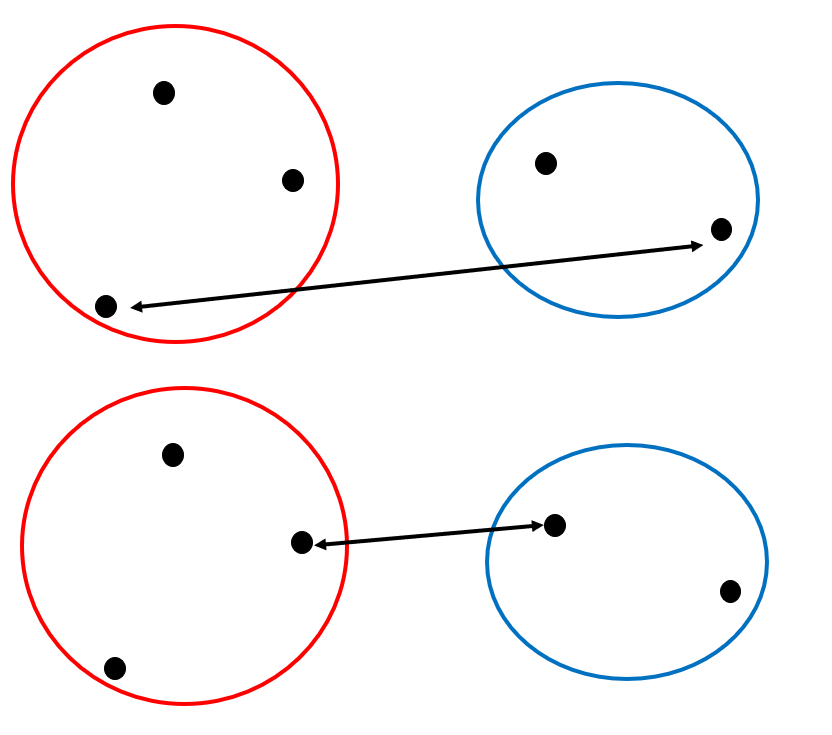
機械学習でよく耳にする「分類(classification)」と「クラスタリング(clustering)」は、どちらもデータ群を分類する手法であるため混同されることがあります。
クラスタリングは教師なし学習であるのに対して、分類(クラス分類)は教師あり学習です。
その違いは以下の図のように表すことができます。
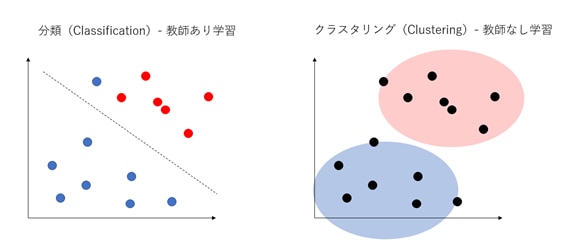
このように、クラスタリングは特徴づけられていないデータをどのようにグルーピングしていくのかが問題になります。
クラスタリングの活用場面
クラスタリングは多くの場面で活用され始めています。
- マーケティング活用(市場調査や顧客情報分析)
- アンケート分析
ここでは、以上の二つを紹介していきます。
マーケティング活用(市場調査や顧客情報分析)
マーケティングでは、ターゲット層を特定することが最も重要なことだと言われています。
セグメンテーションを行うことによって、自社の製品やサービスが最も適した市場を導き出すことができ、より効果的なブランディング、マーケティングを行うことができます。
セグメンテーション(segmentation)は日本語で「区分」といった意味を持ちます。
マーケティングにおけるセグメンテーションは、市場に存在する顧客を特性などに応じて市場を細分化するプロセスのことです。
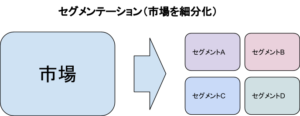
セグメンテーションを行うと、細分化された市場から潜在的なニーズを発見することがあります。これによって、ニーズに合う新しい製品やサービスの開発、既存製品の改善などを行うことができるのです。
しかし、セグメンテーションにおいてセグメントを作成するの様々な基準から判断して作成する人間であり、より細分化できるグループを見失う場合があります。
クラスタリングを活用すれば、セグメンテーションでは発見できなかったニーズを見つけることが可能で、マーケティングの分野で活用されています。
アンケート分析
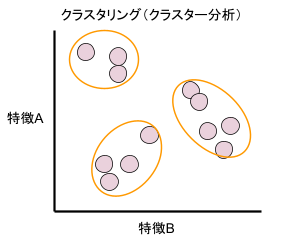
アンケート結果でクラスタリングを行うと、何も見えてこなかった状態から類似性のある者同士で分類することができます。クラスタリングによって分類されたグループに対して、効果的な対策を行いやすくなります。
クラスタリングの2つの手法
クラスタリングは、大きく分けて階層クラスタリングと非階層クラスタリングの2種類に大別されます。
階層クラスタリング
基本的な階層クラスタリングの方法では、適当な点に最も近接しているデータを順番にクラスタリグしていき、それを階層として一つの構造にまとめます。その構造は、端的に言ってしまえば樹形図となります。
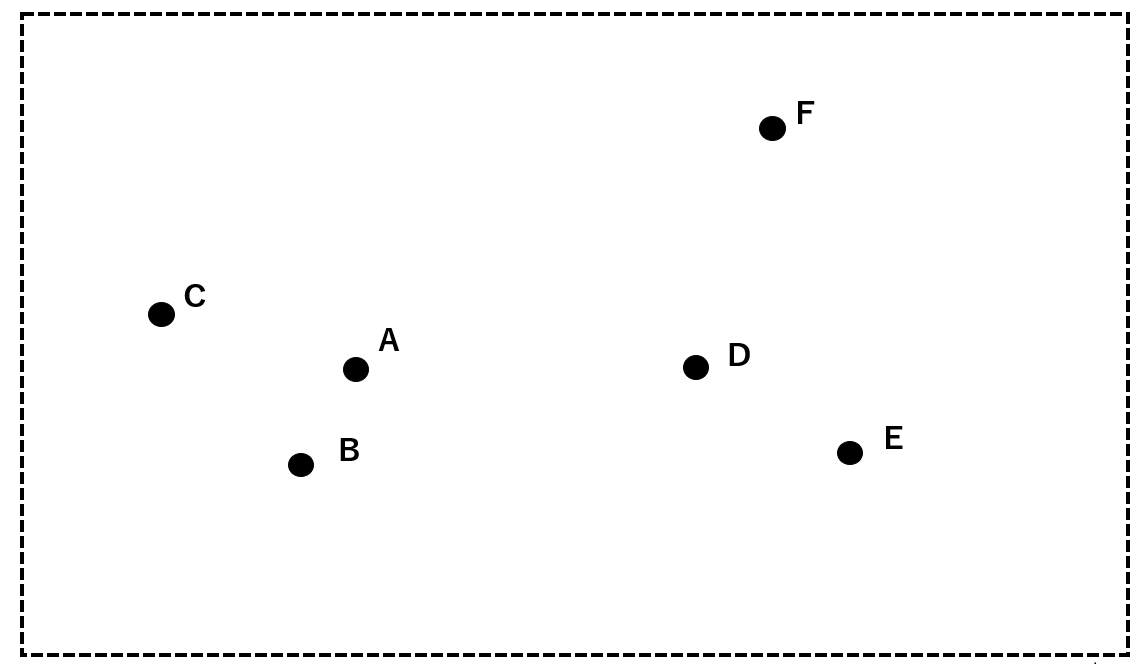
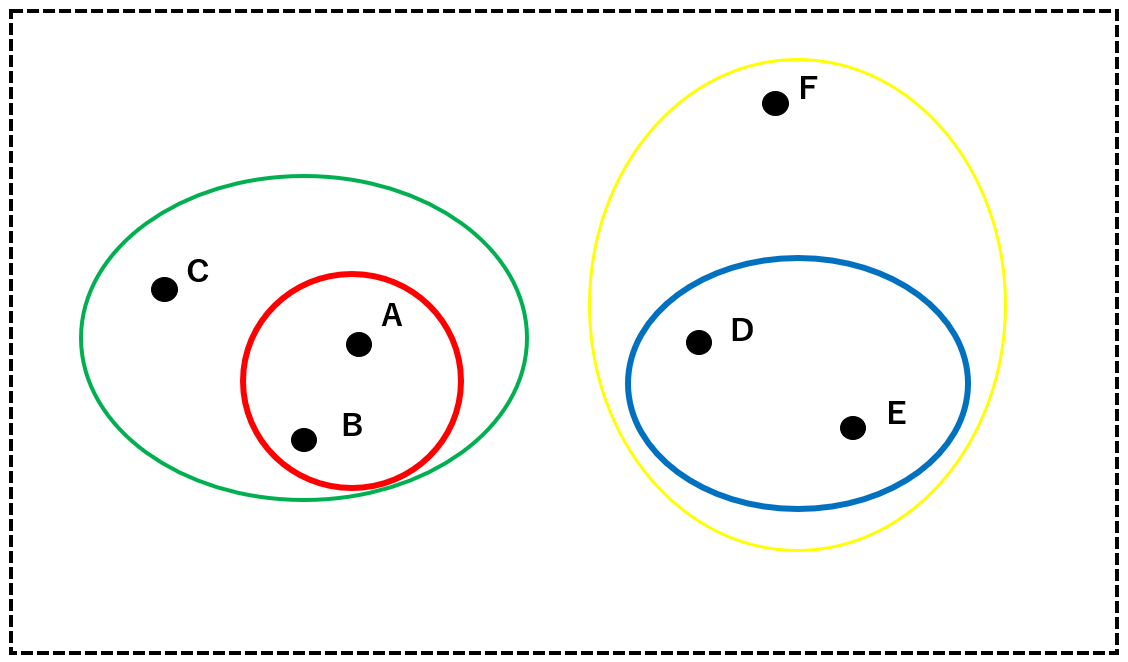
では、実際に以下のA~Fのデータを用いて階層クラスタリングの方法を順に追っていきましょう。
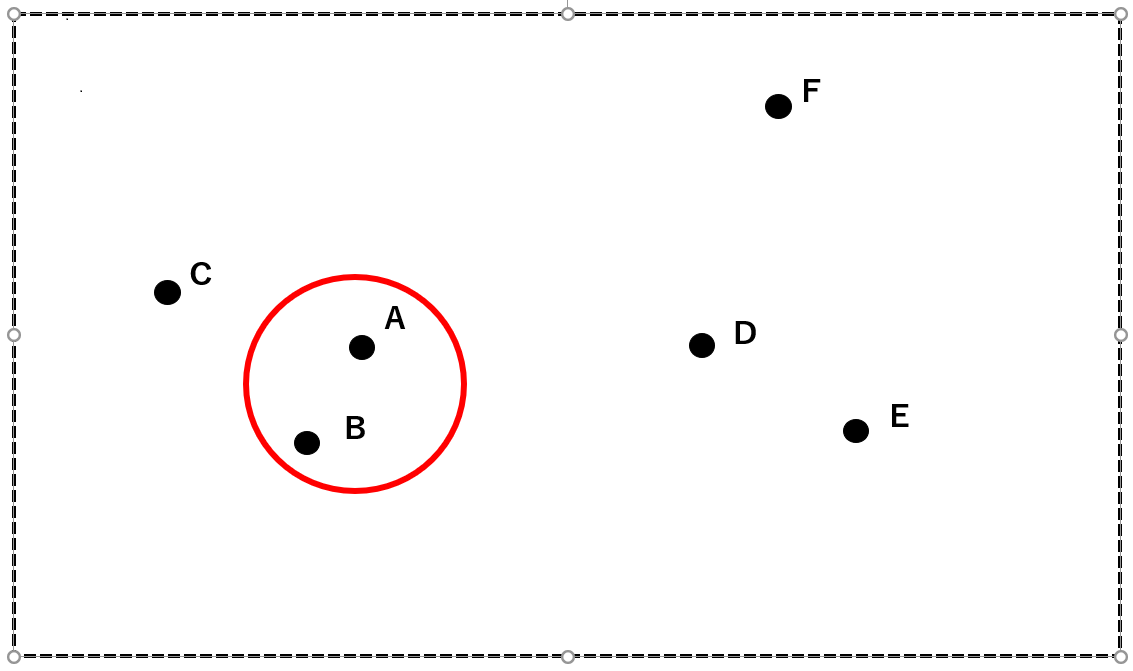
まず、最も近接しているAとBを一つのクラスタにまとめます。
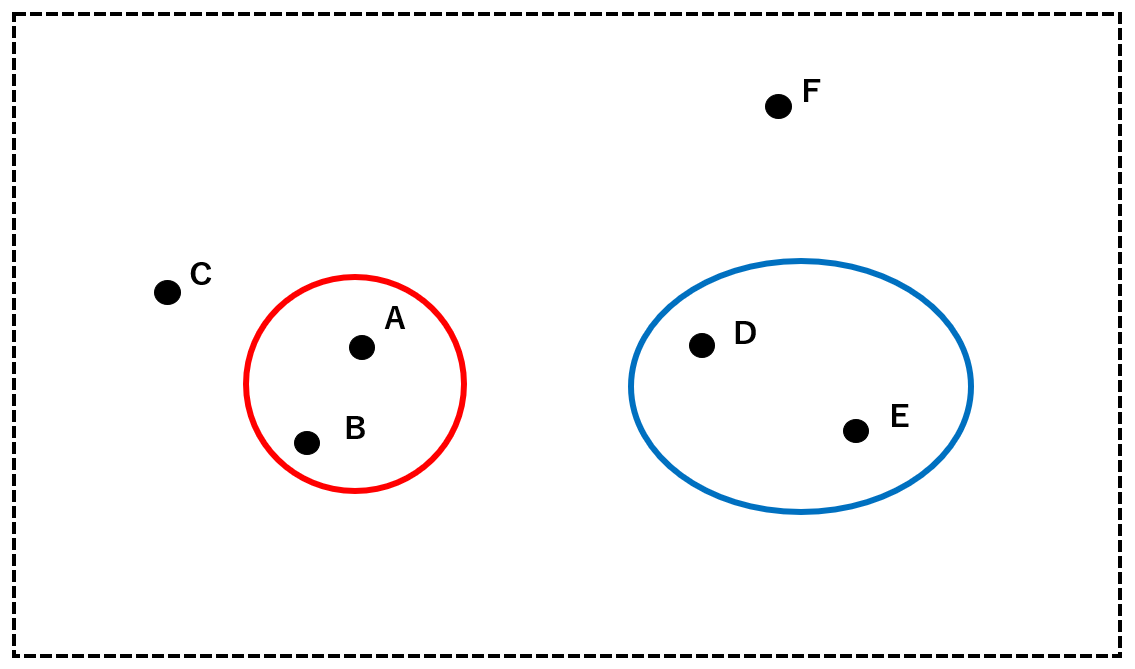
次に、AとBからなるクラスタ(赤)とC, D, E, Fの中から最も近接している2者を一つのクラスタにまとめます。ここでは、DとEをクラスタ(青)にします。
続いて、クラスタ(赤)、クラスタ(青)、C、Fの中から最も近接している2者を一つのグループにまとめます。ここでは、クラスタ(赤)とCをクラスタ(緑)にまとめます。以下同様に、クラスタ(青)とFをクラスタ(黄)にまとめます。
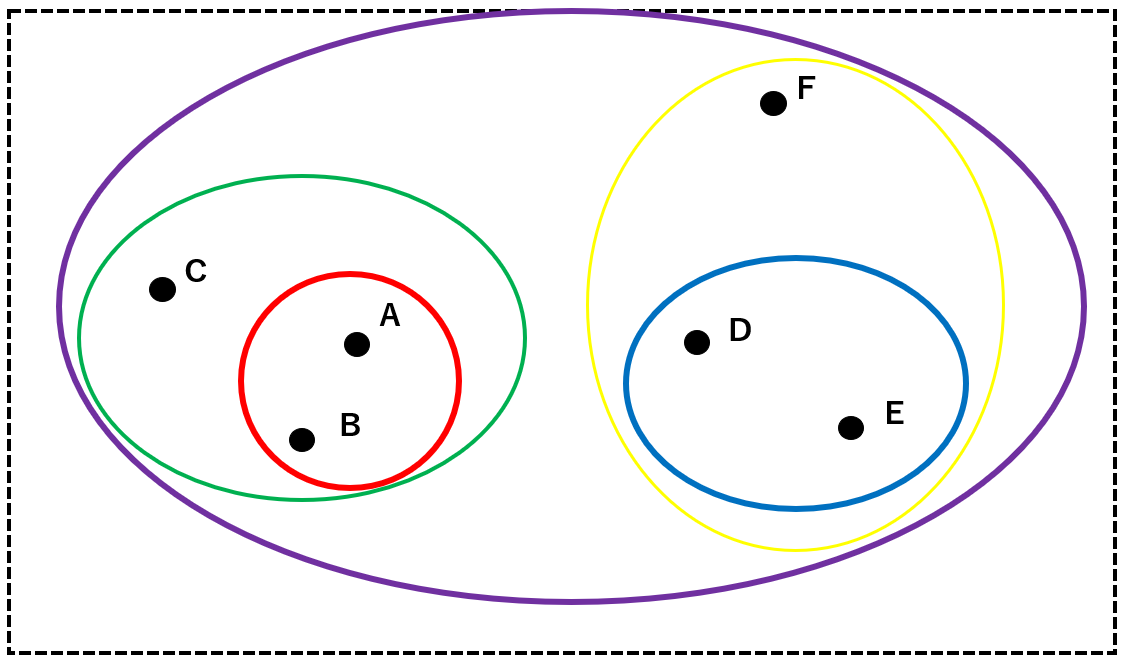
最終的に、すべてのクラスタを包摂するクラスタ(紫)を定めて分析を終了します。
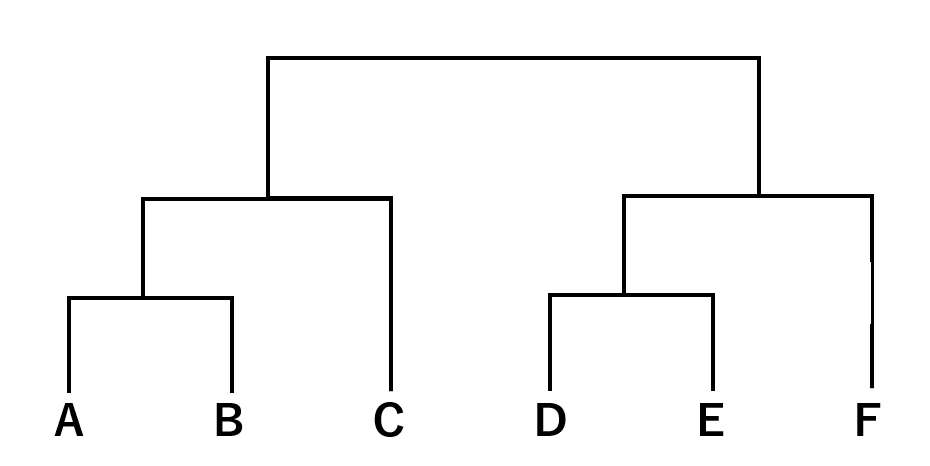
これらの構造を階層に表すと、以下のような樹形図になります。
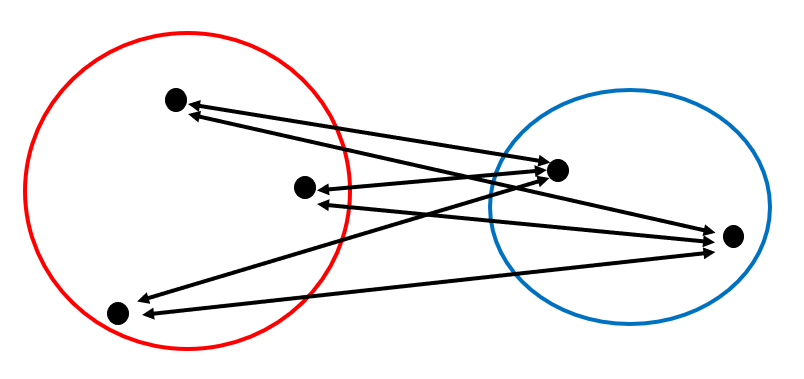
今回の例では「2者がどのくらい近接しているか」を厳密に定義せずに話を進めましたが、その「クラスタ間距離」を決める方法にはいくつかのバリエーションがあります。
群平均法
群平均法は、クラスタを構成するサンプル間距離の平均をクラスタ間距離とする方法です。精度を狂わせる要因である外れ値や異常値に強く、分析が安定しています。そのため、クラスタ間距離を定める方法として、一般的に用いられる手法です。
最長距離法・最短距離法
あるいはシンプルに、各クラスタを構成するサンプルの中で最も遠いもの同士の距離をサンプル間距離とする手法を最長距離法と言います。また、最も近いもの同士の距離をサンプル間距離とする手法を最短距離法と言います。
これらの手法は計算量が少ない一方で各々にデメリットを抱えているため、実際に用いられることはあまり多くありません。
ウォード法
結合前のクラスタ内の全てのサンプルと重心間の距離についての2つのクラスタの和と、結合後のクラスタ内の分散との差が最小になるような、新たなクラスタを作る手法をウォード法と言います。この手法は、精度が優れている一方で計算量が非常に大きくなってしまいます。
非階層クラスタリング
非階層クラスタリングとは、その名の通り、データを階層的な構造(樹形図など)にまとめることなくクラスタに分類する方法です。
前述の階層クラスタリングでは、考えられる組み合わせをすべて計算しなくてはならないため、計算量が膨れ上がり、ビッグデータの解析には適していないとされています。
非階層クラスタリングでは、分類するクラスタの数をあらかじめ人為的に定めてから計算の分析を開始します。その最も代表的な手法として、k-means法が挙げられます。
k-means法
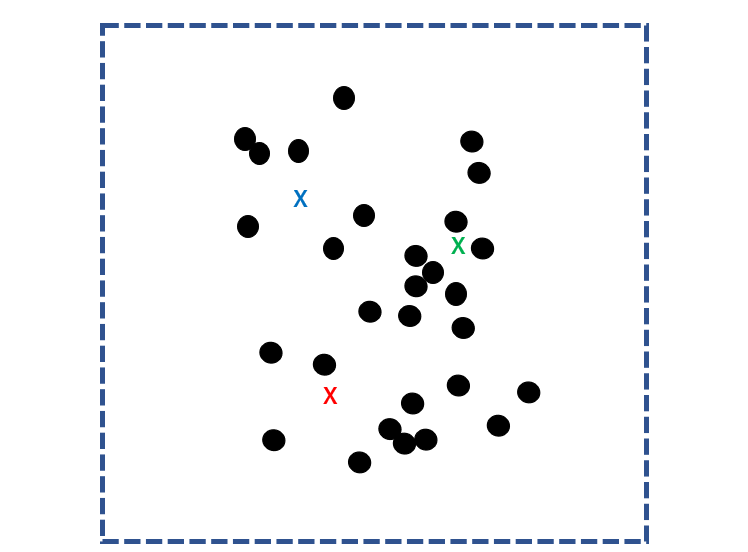
k-means法では、まずサンプルの集団に対してランダムにk個の重心点(核)を定めます。
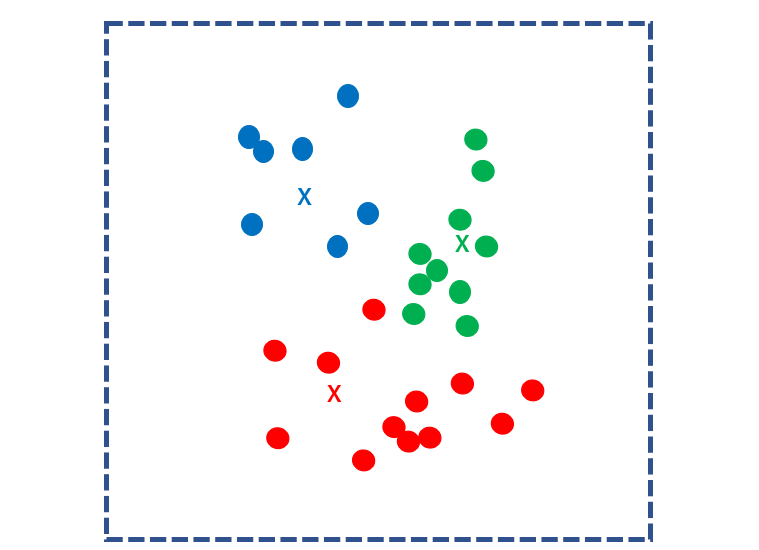
すべてのサンプルとk個の核との距離を計算し、各サンプルを最も近い核に分類します。
次に、クラスターごとの重心点を求め、それを新たなk個の核にします。再びすべてのサンプルとk個の核との距離を計算し、各サンプルを最も近い核に分類します。
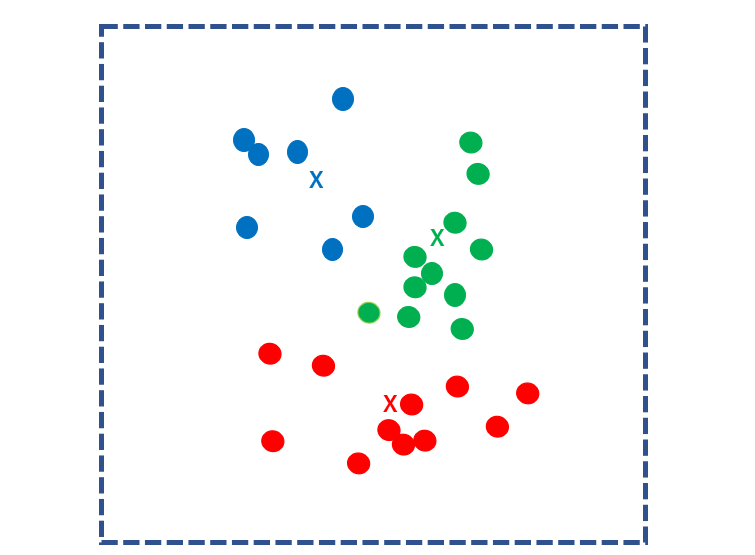
このステップを重心点が移動しなくなるまで繰り返します。重心点が更新されなくなったとき、計算は終了です。
クラスタリングの5つの手順
クラスタリングを効率的に行い有用なデータを得るには、以下のような手順を踏むことが重要です。
- 目的を設定する
- 手法を選ぶ
- 類似度の算出方法を定義する
- クラスタリングの手法を決める
- 分析結果を解釈する
ここでは、各手順の進め方や注意点について紹介していきます。
①目的を設定する
分析を始める際にクラスタリングを行う目的について確認しましょう。
目的を明確にすることで、クラスタリングでどのような手法を選択すればいいのか、クラスタリングを行う対象について確認することが大切です。
ビッグデータを扱うなど大規模な分析を行う場合に、目的を設定することが大切です。
②手法を選ぶ
次にクラスタリングの手法を選択しましょう。
クラスタリングの手法は「階層クラスタリング」と「非階層クラスタリング」の2つに大別され、どちらも性質が異なるため、目的にあった手法を選択しましょう。
階層クラスタリング
階層クラスタリングは、クラスタ数や初期値などのパラメータ設定が不要で結果を視覚化しやすいという特徴があります。しかしデータ数が多くなると分析の信頼性が低下するためビッグデータの分析にも適していません。
非階層クラスタリング
非階層クラスタリングはビッグデータの分析に最適な手法です。
階層クラスタリングと違って、クラスタ数や初期値などのパラメータ設定が必要なため、求めている結果を得るためにはパラメータチューニングが必要です。
③類似度の算出方法を定義する
手法を選んだら、類似度の算出方法を定義しましょう。
クラスタリングは、各データとの距離から類似性を見つけます。距離が近ければ類似度が高いため、同じクラスターに分類される可能性が高くなります。
この距離の定義は複数あるため、クラスタリングを行うデータによって適切なものを採用する必要があります。
ユークリッド距離、マンハッタン距離、チェビシェフ距離など様々な距離から適切な距離を定義し、クラスタリングの信頼性を高めましょう。
④クラスタリングの手法を決める
算出方法を定義したら、クラスタリングの手法を決めましょう。
②でクラスタリングは階層クラスタリング、非階層クラスタリングに大別されることに触れました。階層クラスタリングと非階層クラスタリングはさらに複数の形成方法があります。
階層クラスタリング
- ウォード法
- 群平均法
- 最短距離法
- 最長距離法
非階層クラスタリング
- k-means法
- 超体積法
⑤分析結果を解釈する
最後にクラスタリングの分析結果から考察を行いましょう。クラスタリングの結果のままでは、クラスターごとに分けられただけです。その結果から考察し、正しく解釈することによってクラスタリングの結果を有効に活用することができます。
クラスタリングのメリットとデメリット
数ある機械学習の手法の中で、クラスタリングは古典的でありながら比較的安定した性能を持っています。以下では、クラスタリングのメリットとデメリットについて述べていきます。
階層クラスタリングと非階層クラスタリングの比較
| 階層クラスタリング | 非階層クラスタリング | |
| 計算量 | 多い | 少ない |
| クラスタ数 | 自由 | 事前に指定する必要がある |
| 固有の問題 | 計算量が多い | 初期値依存 |
先述のように、階層クラスタリングはクラスタ数を事前に決める必要がない一方で、計算量が膨大になってしまいます。したがって、階層クラスタリングはビッグデータの処理には不向きです。
非階層クラスタリングは計算量が少ない一方で、事前に人為的にクラスタ数を指定しなければなりません。
また、k-means法では最初の核(重心点)次第で結果が大きく変わってしまうことがあるため、安定した結果を得ることが難しくなります。この現象を「初期値依存」と呼びます。
次元の呪い
クラスタリングの問題点として挙げられるのは「次元の呪い」です。
次元(説明変数の数)の多いデータを対象に計算する場合、その計算量は次元の数に対して指数関数的に増加していきます。
膨大な次元に対して各データがそこまで分散していないデータ(各次元の相関関係が比較的強いデータ)、あるいはデータ量が少ないものをクラスタリングする場合、「次元の呪い」によって過学習が発生する可能性が高まります。
k最近傍法など、次元の呪いはクラスタリングだけでなく、他の様々な手法にもみられる代表的な問題です。これらの分析では計算の過程で次元数がどんどん増えていくため、過学習が発生しえます。また、ディープラーニングの分野でも同じ問題が指摘されています。
クラスタリングの活用事例
クラスタリングは、樹形図や色の塗分けなどで結果をわかりやすく可視化できるため、マーケティングや商品アピールなどの非技術的な分野でも広く用いられています。
会社や営業の戦略立案
例えば、顧客データを分析することで、属性の似た顧客の集団を分析できます。その集団ごとに戦略を立てて商品や情報をアピールすることで、より効率的なマーケティングが可能です。
あるいは、他社の顧客データと比較することで、自分の会社の顧客がどの集団(クラスタ)に属しているのかを判断できます。こうしたデータをもとに、会社のブランディングを強化できるでしょう。
画像分類・音声分類
画像データや音声データからなるビッグデータをクラスタリングすることで、似た傾向にあるデータを分類できます。
例えば、比較的類似したリズムや調性を持つ音楽を分類することで、「夜に聴く音楽」や「気分を上げたいときに聴く音楽」といった属性を持つクラスタを作り出すことが可能です。
まとめ
クラスタリングはシンプルでありながら複雑な分類問題にも対応しており、マーケティングやアンケート分析など今後多くの分野で使用されていくことでしょう。
一方、次元の呪いに代表されるようなAIの問題も抱えています。こうした問題を克服する試みは続いており、クラスタリングの発展が期待されています。
この記事がクラスタリングの理解に少しでもお役に立てれば幸いです。