最終更新日:

ある特定の課題を解決できる能力を、人間並みか、人間を上回る精度でAIが学習することは、深層強化学習によって実現しつつあります。この深層強化学習モデルは、報酬体系の異なる複数の課題を解決することができるMulti-task learningを行うことができつつあります。
しかし、問題状況が、動的に時々刻々とリアルタイムに変容していくなかで、状況の変化に即して、変化したあとの新たな状況にうまく適合した新しい問題解決動作を瞬時に繰り出すことができる能力を深層強化学習の枠組みでどのようにAIに学ばせるのかについては、今後の課題なのではないでしょうか。
この文脈では、Meta-learningが、「ある特定の課題を解決できる能力(動作)」を身につける方法それ自体を、AIに学ばせる学習方法として、一部で注目を集めています。Meta-learningがAIに学習させる対象は、「個々の課題を解決するための方法(動作)」を学ぶ「方法」であるという意味で、メタ・レベルの「方法」であるということになります。
ところで、「問題状況が、動的に時々刻々とリアルタイムに変容していくなかで、状況の変化に即して、変化したあとの新たな状況にうまく適合した新しい問題解決動作を瞬時に繰り出すことができる能力」を発揮することができる数理モデルとしては、非平衡系(系の内外で、情報とエネルギーの出入りがあるような動的な系)の環境下で、無秩序から秩序(アトラクタ)が自己組織化的に成立しては、系の内外の情報とエネルギーが変化していくのにあわせて、別の秩序(アトラクタ)へと自律的に遷移していく自己組織化のモデルがあります。
ここでは、非平衡系のなかで、ある時点において、自己組織化的に成立している「秩序(アトラクタ)」が、その時点で系全体が帯びている状況にうまく適応した問題解決動作(問題解決能力)に相当します。
自己組織化モデルでは、系全体の状況が変化していくのにあわせて、変化した後のあらたな状況に適応したあらたな「秩序(問題解決動作・問題解決能力)」が、自然発生的に成立してくる部分があります。
こうした特性は、Meta-learningが目指しているところであるのではないでしょうか。
この記事では、この自己組織化的なアトラクタ・モデルを、環境のなかから感覚・行動系を自律的に獲得していく能力をもつ数理モデルとして実装することに成功している東京大学の国吉・新山研究室の取り組みに着目することで、その可能性に光を当ててみます。
同時に、この特性を獲得するために、Meta-learningが新たに乗り越えなければならない課題がどのあたりにあるのかについても、考えてみたいと思います。
目次
- 深層強化学習は、AI開発者が選定した特定の問題解決動作能力をAIに学ばせることができるようになった
- 複数のタスクの問題解決能力を学習可能な深層強化学習も出現しつつある
- Meta-learningモデルの研究動向
- アトラクタ遍歴モデルの特徴
- 「真の発達原理」・「真の知能の原理の解明」を構成論的に理解するアプローチ
- Meta-learningモデルとアトラクタ遍歴モデルの相違点
- 国吉・新山研究室:カオス結合場としての身体性に基づく行動創発
- 深層学習モデルや深層強化学習モデルとの比較
- Meta-learningも「一つの渦」を学習させるモデルに留まるものか?
- One-shot / Zero-shot learning vs. アトラクタ遍歴モデル
- 迷路のゴールに至る最短経路問題におけるカオス理論の適用例
- 国吉・新山研究室で進行中の研究領域
- 周期運動のモデル化は、「神経振動子」を用いた松岡モデル等が有名
深層強化学習は、AI開発者が選定した特定の問題解決動作能力をAIに学ばせることができるようになった
状態価値ベースの深層強化学習モデルと、モンテカルロ探索木を組み合わせた手法で構築されたAlphaGoは、人間のトップ棋士に連戦連勝する成績を出していますし、その後継モデルのAlphaGoZeroは、過去に人間の囲碁棋士どうしの対戦データである棋譜を学習データとして与えなくても、AIを自己対戦させることで、教師なしで囲碁の一手を繰り出す力を洗練させていくことができることを証明しました。
さらに、AlpaZeroは、1つのモデルが、囲碁と将棋など、複数の碁盤ゲームの対局に臨むことができるようになりました。
また、行動価値ベースの方策勾配関数を用いた深層強化学習モデルは、離散値ではなく、連続的な座標地点で構成される物理空間のなかで、障害物をかろやかに飛び越えたりするような、俊敏な身体動作を発揮することのできるAI Agentを実現させています。
複数のタスクの問題解決能力を学習可能な深層強化学習も出現しつつある
こうした深層鏡学習モデルは、それぞれ異なる報酬体系をもつ複数の課題を学習し、覚えることのできる能力をも獲得しつつあります。その1つが、Googe DeepMindが公表したPopArtモデルです。
(論文)
- Matteo Hessel et.al., Multi-task Deep Reinforcement Learning with PopArt, AAAI’19
- Hado van Hasselt et.al., Learning values across many orders of magnitude, NIPS’16
(解説ウェブページ)
- Gigazine誌 (2018年09月14日) 「AIのマルチタスク学習時に生じる報酬の差異を埋めるための技術「PopArt」をDeepMindが開発」
- Reiji Hatuga [DL輪読会]大規模分散強化学習の難しい問題設定への適用
Meta-learningモデルの研究動向
Meta-learningについては、関連する隣接領域との関係を含めて、次のスライドが参考になります。
取り上げているのは、こちらの論文です。
アトラクタ遍歴モデルの特徴
数々の異なる知的能力と運動能力が、連続的に発生してくるダイナミズムを総体的に解明する方向性を打ち出している
自己組織化モデルは、当初成立していた系(の状況)が時々刻々と変容して、新たな系(の状況)に様変わりしていくのにあわせて、系がもつ秩序の方も、もともと成立していた系(の状況)に適応していた「秩序(問題解決動作・問題解決能力)」から、変化した後のあらたな系の状況に適応したあらたな「秩序(問題解決動作・問題解決能力)」へと、しなやかに変化していく特性を発揮するモデルである、と紹介しました。
このような特性をもつ非平衡系の自己組織化の数理モデルがもつ特徴を、深層強化学習モデルを含む機械学習モデルと比較する視座のなかで論じている論文として、東京大学の国吉・新山研究室の次の文章があります。
この文章から要点となる文をいくつか抜粋して紹介します。なお、以下に抜粋する文章中の改行は、小野寺によるものです。
(小野寺注:知能の)発達システムにおいて、特定の機能の仕組みを論ずるのではなく、多様な知的機能がどのように発生し変化していくか、その仕組みを解明し構成しようというものである。
発達システムにおいて、ある瞬間のシステムの機能や構造は、そのシステムの動作原理とは直接対応つかない。なぜなら、発達システムの動作は「変化すること」だかである。例えるならば、発達システムは「流れ」であり、ある瞬間の機能や構造は「渦」といえる。
従来のAIや認知ロボティクスの方法は、静水中に渦の型を入れたあと、適当な水流を起こして意図した渦の発生と維持を期待することに近い。
(中略)
従来の認知発達ロボティクスでは、模倣機能や道具使用機能といった特定の認知機能を対象とし、それらが発達の特定のフェーズにある認知システム上でどう獲得されうるかを研究対象としてきた。
人間の認知機能全体、発達の全域を扱うことなどできないから当然とされた。
この場合、対象学習フェーズ初期の認知システム機構を明示的に作り込み、その上で学習により所期の認知機能を獲得しうるかという問題設定となる。
このアプローチでは、実験が成功すればあらかじめ想定したとおりの仕組みで想定したとおりの発達が起こるのであり、人間の認知の仕組みについての新たな知見を提起する可能性は少ない。
前述の渦の例に戻ると、1個の渦の生成消滅のみに限定してモデル化し再現しようとするのは無理がある。多様に変化する渦すべての発生の根本原理を明らかにし、その原理に従う系を構成することが本質に迫る方法である。
(中略)
この議論を極限まで進めるならば、真の発達原理を明らかにするためには、発達の原初から発達経過の全域にわたって連続的に変化するシステムを構成する必要がある。
人間の発達であれば、究極的には受精卵を起点とする全人生を生成できる原理を求めるべきである。その達成は遠い将来の目標としても、現状の技術で可能な限り初期からの連続的発達をモデル化する試みが、真の知能の原理の解明に向けて特に重要と考えられる。
「真の発達原理」・「真の知能の原理の解明」を構成論的に理解するアプローチ
小野寺も、「究極的には受精卵を起点とする」「発達の原初から発達経過の全域にわたって」、以下のような様々な運動能力や知的能力が、「連続的に変化するシステム」のなかで、「連続的に」どのようなダイナミズムを発揮するいかなるメカニズム(作用機序)によって、ある特定の順序をたどりながら生成・出現してくるのかを理解することこそ、「真の発達原理」・「真の知能の原理の解明」につながるのだと考えます。
今日、DeepMindや(イーロン・マスク氏やベン・ゲーツェル氏が創設した)非営利研究企業・OpenAIによって牽引される形で、「IBM Watson」や「アルファ碁」や「無人自動車」を実現するなどの数々の目覚ましい成果を上げているディープ・ラーニングモデルを含む機械学習や統計的学習理論モデルは、上述の国吉教授の表現を借りるならば、いずれも、ある「対象学習フェーズ」段階における「ある瞬間のシステムの機能や構造」を人間である研究者や開発者であるが天下り的に取り出した上で、その特定の「機能や構造」を挙動として表現しうるAIアルゴリズムとして、見いだされたアルゴリズム(=計算手順。ないしは数理表現)モデルです。
そのように、天下り的に人間によって選択された、特定の「学習フェーズ」について、「対象学習フェーズ初期の認知システム機構を明示的に作り込み、その上で学習により所期の認知機能を獲得しうるかという問題設定」のもとで生み出されたアルゴリズム(モデル)は、それがどんなに優れたパフォーマンスを発揮するアルゴリズムであったとしても、「このアプローチでは、実験が成功すればあらかじめ想定したとおりの仕組みで想定したとおりの発達が起こるのであり、人間の認知の仕組みについての新たな知見を提起する可能性は少ない」のです。
Meta-learningモデルとアトラクタ遍歴モデルの相違点
機械学習を含む統計的数理モデルを設計する際、AIモデルに、どのような課題の解法を学ばせるのかは、AIモデルの設計者である人間が決定します。
Meta-learningは、「複数の課題」を精度よく解決するための方策を学ぶ「学び方」を(メタ的に)学習させるものですが、このとき「複数の課題」として、どのような課題を選ぶのかは、人間が選択することになります。
ここで行われていることは、先ほどの国吉ほかの論考の言葉を借りると、Meta-learningモデルに対して、どの「学習フェーズ」のどのような「課題」の解決方策の「学び方」をAIモデルに学習させるのかを、AIモデル自身に動的・自律的に選択させるのではなく、
AIモデルに対して、人間が天下り的に決定しているということになります。
これは、「対象学習フェーズ初期の認知システム機構を」人間が「明示的に作り込み、その上で学習により所期の認知機能を獲得しうるかという問題設定」をしていることになります。
先の論考の言葉を借りると、「このアプローチでは、実験が成功すればあらかじめ想定したとおりの仕組みで想定したとおりの発達が起こるのであり、人間の認知の仕組みについての新たな知見を提起する可能性は少ない」ものになります。
「変化すること」をその本質とする「発達システム」において、「多様な知的機能がどのように発生し変化していくか、その仕組みを解明し構成しようと」するためには、
「1個の渦の生成消滅のみに限定してモデル化し再現しようとするのは無理がある。多様に変化する渦すべての発生の根本原理を明らかにし、その原理に従う系を構成することが本質に迫る方法である」のです。
ここで、「渦」とは、「流れ」である「発達システム」において生じる、『ある瞬間の機能や構造』のことを指していました。
国吉らが取るアプローチは、生命活動との比喩でいえば、ひとつの胚(受精卵)から、細胞分裂を繰り返すなかで、じょじょに、様々な身体動作機能や知的情報処理機能(アルゴリズム)を担う細胞群が、自己(細胞)と周囲の環境との間で生じる相互作用の積み重ねのなかで、
自己組織化的に、自然発生的・内発的に発芽してくるような流れをとります。
そこでは、どのような(複数の)課題の解法方策の「学び方」を(メタ的に)AIモデルが学習すべきかは、天下り的に人間がAIモデルに対して与えるのではなく、AIモデルが身を置いている行動環境とAIモデル自身との物理的な相互作用のなかで、AIモデル自身が、自己組織化論的に、カオスから秩序(アトラクター)が自然発生するダイナミズムによって、自ら自律的に選び取っていく方法が追求されているのではないでしょうか。
AIモデルの開発・設計者である人間が、(AIがお手本とするべき)人間の知的機能や体の運動能力を、個々の単体の機能(能力)に1つ1つばらばらに切り出した上で、切り出した個々の単体の機能を「人間並み」・「人間を超える精度パフォーマンス」で実現するAIアルゴリズムを個別に(独立して)設計した上で、人間の手で、それら個々の機能を発揮するアルゴリズムを、電子基板上で個々の機能素子(モジュール)を電子回路上でつなぎ合わせるように、あとから結合させることで、あらゆる問題課題を解決しうる汎用人工知能エージェントを生み出そうとしているのが、現在主流のAI研究の流れです。
そこでは、最初に人間が天下り的に、知性を構成する個々の機能を定義しています。
それに対して、国吉らは、「受精卵」のような「たったひとつの胚」から、あたかも内側から自発的に(つまり、アルゴリズム自身のダイナミズムだけで)個々の異なる機能を担う複数のAIモジュール領域が内発的に自然発生してくる、細胞分化型とも形容すべきアプローチを目指していると捉えることができます。
そこでシミュレーションの実証実験を通して追求されるのは、人工的なAIロボットが、当初は感覚器官も運動器官も未だ未分化な「胚」の状態から、行動空間のなかで手足(四肢)を適切に動かすのに必要となる感覚・運動系を少しずつ自己組織化論的に獲得し、行動環境が変化すると、「秩序層(ある状況に対して適合的な身体動作・問題解決方策を実行する挙動を示すアトラクター)」から「無秩序層(意味ある挙動を示さなくなる状態)」を経て、別の秩序層(新たな状況に対して適合的な身体動作・問題解決方策を実行する挙動を示すアトラクター)へと自律的に遷移していくダイナミズムが成立するための(非線形数理モデルにおける)パラメータの条件集合に関する知見です。
Meta-learningとの関係では、時々刻々と変化していく行動空間のそのときどきの瞬間における状況にあわせて、AIモデル自身が、どのような行動とどのような行動の束を、学ぶべきかを自己判断し、それら複数の行動を「学び取る方法」(学習法の学習:メタレベルの学習(learning))を学ぶという課題設定を、人間から天下り的に与えられるのではなく、AI Agent自身が自律的・内発的に、自己組織化的に行うようなダイナミズムが探求されています。
国吉・新山研究室:カオス結合場としての身体性に基づく行動創発
国吉・新山研究室は、「カオス結合系」が生じる「場」を、センサーとモーターで構成されるメカニカルな身体をロボット(AI Agent)に組み込む問題設定を設計しています。
このようなロボットは、自己の身体の各部分のあいだ(四肢と関節と坐骨、など)に、情報とエネルギーの相互作用が絶えず生じており、その相互作用は時々刻々と変化しています。そのような要素と要素が互いに影響を及ぼしあいながら、ダイナミックに変化していく「場」のなかに、ロボットは身を置いています。また、ロボットは、自己の身体全体と周囲の物理環境との間にも、同種の時々刻々と変化する動的な相互作用の流れを体感しています。
このような外部と内部との間で、動的な情報とエネルギーの流れが生じている物理系を、非平衡系と呼びます。この非平衡系が舞台として存在した上で、さらに自由度の数など、いくつかの条件が揃った系において、カオスから秩序(アトラクター)が生じては、また別の秩序(アトラクター)へと自然発生的に(内発的に)移り変わっていく(遷移していく)現象が生じてきます。
このようなカオス系どうしが、互いに影響を及ぼし合う「カオス系を要素にもつ系」は、「カオス結合系」(参考)と呼ばれていますが、国吉・新山研究室では、この「カオス結合場」としての身体性を備えたロボットの身体から、時々刻々と変化する状況に適応する行動が自己組織的に創発しては、別の行動へと自然発生的に遷移していくダイナミズムを、数理モデルのシミュレーションで実証的に観察していく研究に取り組んでいます。
このような取り組みから、動的に変化する行動環境のなかで、取るべき行動を瞬時に(自然発生的に)切り替えていく振る舞いを示すことができる人工生命体が発生するための数理的な条件の組み合わせについて、着々と知見を積み上げています。
3.1.2 相互作用場としての身体・環境
カオス結合系が発生する多様なクラスタ構造は、多自由度系の多様な協調関係と見なすことができる。さらに、カオス的遍歴現象は、我々が求める、複数の(疑似)アトラクタを移り歩く機能そのものである。これをロボットに当てはめれば、多自由度の運動の非常に多様な協調パタンに部分的に引き込まれつつ、自発的に移り変わっていく能力が実現できるのではないか。
このような直観をもとに、我々は、身体性を結合場とするカオス結合系という新しいモデルを提案した[32](Fig.1).
このモデルでは、カオス要素の出力に応じて身体のアクチュエータを駆動し、センサ値をカオス要素に入力する。アクチュエータの駆動は身体全体の物理状態に影響を与え、各センサに影響を与える。つまり、各写像は身体全体の動力学、つまり時間変化する非線形関数により結合される。しかも、身体は常に環境と接し、相互作用しているので、この結合関係は身体-環境相互作用の状態を時々刻々反映している。
これは元来のCML/GCMのような時不変の結合ではなく、時変の非線形な結合場となり、その振る舞いを理論的に予測することは極めて困難である。
しかし、次のことが直観的に期待できる。カオス要素間の部分的協調は、身体のいくつかの関節を協調させ、一つの身体運動パタンを発生させる。また、この協調パタンは、身体性と環境状態に呼応して決まる。したがって、身体の構造や、環境状態の変化に呼応して、身体運動は変化する。つまり、適応性を示す可能性がある。これを実験的に確認していく。
以上、引用した部分で言及されているFig.1とは、以下の図版です。
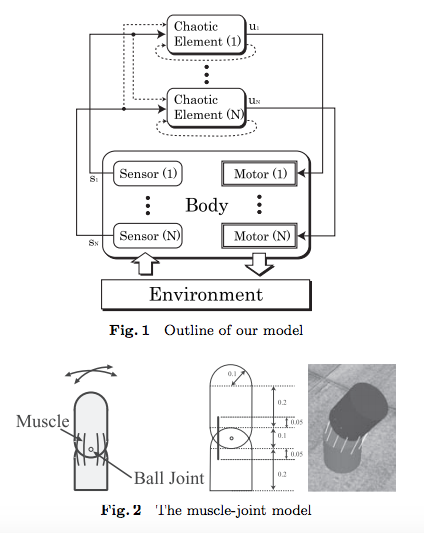
国吉ほか「人間的身体性に基づく知能の発生原理解明への構成論的アプローチ」,日本ロボット学会誌 Vol.28, 2010年よりFig.1およびFig.2を転載。
国吉教授ほかは、胎児と幼児の身体を模擬した数理モデルとして、以下のFig.9に描かれた筋肉・関節・神経系を持つ身体系のモデルを用意します。
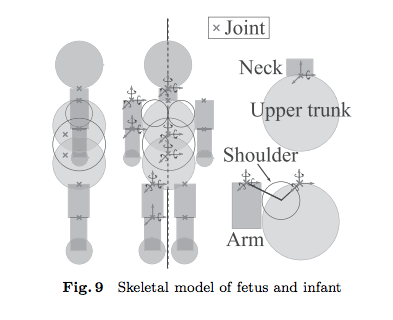
国吉ほか「人間的身体性に基づく知能の発生原理解明への構成論的アプローチ」,日本ロボット学会誌 Vol.28, 2010年よりFig.9を転載。
その上で、以下のような壁で囲まれた物理空間のなかにいる新生児が、物理的に床と四方の壁に取り囲まれているという物理的な制約条件と、新生児の感覚・運動系(神経・関節・筋肉系)が動的に相互作用しつつ、時系列でみて、系全体(=身体全体)としてどのような動き(挙動)を示すのかを、シミュレーション実験を行い、検証しています。
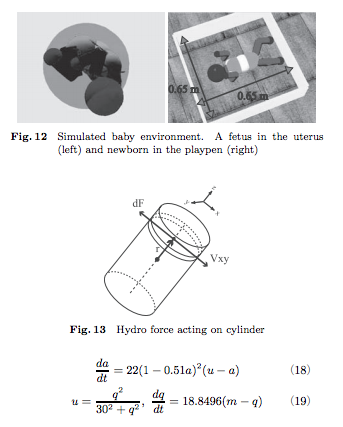
国吉ほか「人間的身体性に基づく知能の発生原理解明への構成論的アプローチ」,日本ロボット学会誌 Vol.28, 2010年よりFig.12を転載。
そのシミュレーション結果は以下のとおりであると、報告しています。
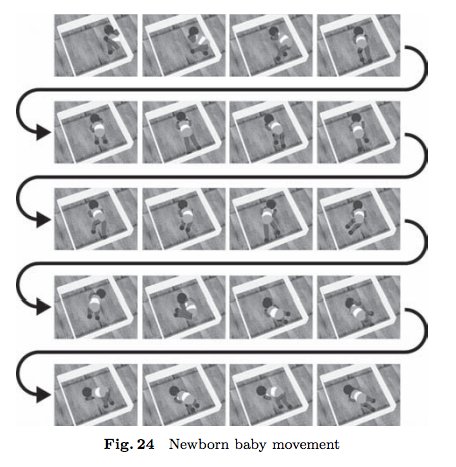
国吉ほか「人間的身体性に基づく知能の発生原理解明への構成論的アプローチ」,日本ロボット学会誌 Vol.28, 2010年よりFig.24を転載。
深層学習モデルや深層強化学習モデルとの比較
国吉教授はさらに、先に引用した文章を盛り込んだ論考のなかで、「究極的には受精卵を起点とする」「発達の原初から発達経過の全域にわたって」、様々な運動能力や知的能力が、「連続的に変化」しながらある順序をたどりながら生成されてくる「システム」でないと、あらかじめ想定されていない未知の行動環境や問題環境に、「汎用的に」対応・対処することのできる知的なAIは、実現しえない、という考えを示しています。
この見解は、今日、DeepMindや(イーロン・マスク氏やベン・ゲーツェル氏が創設した)OpenAIによって牽引される形で、「IBM Watson」や「アルファ碁」や「無人自動車」を実現するなどの数々の目覚ましい成果を上げているディープ・ラーニングモデルを含む機械学習や統計的学習理論モデルが、いまだに乗り越えることができずにいる限界であり、課題であると、国吉教授は述べています。
このあたりの見解が述べられた文章を、先の論考から引用してみます。
2章で提案した原初の行動発生原理としては、事前に規定されない任意の身体環境
相互作用を発見し、学習が可能な程度の安定化をもたらすのが必要である。
これは強化学習やGA(小野寺注:「遺伝的アルゴリズム」を指す)などの最適化手法では達成できない。
なぜなら事前に規定された基本行動要素や状態表現と評価関数に従って探索を行うため、生成される行動が未知対象のダイナミクスに適合しない可能性があり、また、程度の差はあっても評価関数によって限定された部分空間の探索に留まるからである。
評価関数はタスク依存なので、探索もタスク依存である。このため、未知の多様な状況に臨機応変に適応する能力を実現することは現実には困難と考えられる。
いま世の中の注目を一身に集めている数々のAIモデルは、どれも「特定の」問題領域(タスク領域)のなかで、有用性の観点から高いパフォーマンスを上げるために、「特定の」問題領域(タスク領域)ごとに個別に人間のAI開発者の努力により、(人間によって)作り込まれたモデルであり、人間のAI開発者が想定していなかった問題状況(タスク状況)に、それらのAIモデルの稼働環境が移行すると、そのパフォーマンスは一般に大きく低迷してしまう、ということが述べられています。
Meta-learningも「一つの渦」を学習させるモデルに留まるものか?
なお、複数のタスク(問題状況)に(汎用的に)対応できる対処能力を備えたAIアルゴリズムとしては、冒頭に取り上げたMulti-task learningや、Meta-learningモデルのほか、転移学習モデルなどがあります。
この分野で、この数年間で大きく注目を集めたモデルとしては、一例として以下があります。
- [Google Brain] AutoMLモデル
- [Google DeepMind] PathNetモデル
- [Google DeepMind] Relational Networksモデル
- [Google DeepMind] Graph Networksモデル
- [Google DeepMind] PopArtモデル
- [Google DeepMind] Overcoming catastrophic forgetting in neural networksモデル
しかし、このような一群のモデルも、さきほどの国吉教授の言葉を借りれば、以下の段階にとどまっているのではないでしょうか。
従来のAIや認知ロボティクスの方法は、静水中に渦の型を入れたあと、適当な水流を起こして意図した渦の発生と維持を期待することに近い。
(中略)
この場合、対象学習フェーズ初期の認知システム機構を明示的に作り込み、その上で学習により所期の認知機能を獲得しうるかという問題設定となる。
このアプローチでは、実験が成功すればあらかじめ想定したとおりの仕組みで想定したとおりの発達が起こるのであり、人間の認知の仕組みについての新たな知見を提起する可能性は少ない。
前述の渦の例に戻ると、1個の渦の生成消滅のみに限定してモデル化し再現しようとするのは無理がある。
つまり、Meta-learningモデルが学ぶべき「問題解決行動を獲得する方法」を学ぶ(メタレベルでの)「方法」を、AIモデルの設計者・学習条件の設定者である人間が人為的に選択して、AIに与えているのではないでしょうか。
このようにして生み出されたAIモデルが、しかし、人間によって与えられていた学習対象(特定の「問題解決行動を獲得する方法」を学ぶ(メタレベルでの)特定の「方法」)の範囲を超えて、モデルの学習段階で学習データとして与えられてはいなかった新しい領域の問題解決行動を獲得する方法までも、メタレベルで学習する能力を発揮するとしたら、ある「アトラクタ」から別の「アトラクタ」へと動的に、自律的に自己を変容させうる自己組織化モデルの挙動に近づいてくるのかもしれません。
「身体」を「カオス結合系」と見立てた国吉らの身体をもつAIモデルは、急に障害物が発生したり、行動空間構造が変わったり、行動ルールが突然、何の前触れもなく急変したとしても、あらたな状況をAIに「学習させて」学ばせることなく、即座に状況の変化に即応的に対応することができるAIモデルを、運動・神経系の自己形成モデルや自己身体表象の獲得モデルとして、すでに複数、開発しているようです。
One-shot / Zero-shot learning vs. アトラクタ遍歴モデル
なお、ディープ・ラーニングモデルを中心とする機械学習モデルの方法論の内部では、Meta-learningモデルとは別に、これまでに遭遇したことのなかった新種や未知の状況に、初めて(1回目に)直面したときでも、新しい状況に関するデータを、1回、センサー等によって検知・知覚するだけで、その新しい状況に即応的に対処する方法を編み出すことができるアルゴリズムの研究が盛んに研究されています。
One-shot learningやZero-shot learningと呼ばれるアルゴリズムがそれです。
これらの名前によって総称されるモデルは、新しい状況に関するデータを、たった1回、センサー等によって検知・知覚するだけで、その状況に対応するために、これまで慣れ親しんだ状況で有効であり続けてきた、すでに体得済みの行動パターンを、部分的に修正や変更を加えることで、臨機応変的に応用することで、新しい状況に適合した新たな行動パターンを、瞬時に生み出すことができる能力を持ったアルゴリズムを指します。
カオス結合系モデルと、これらディープ・ラーニングモデルを始めとする機械学習モデルの方法論をとるOne-shot / Zero-shot learningモデルは、急に出現した新しい状況に対する対応力という点で、パフォーマンスの相互比較をもっと力を入れて行うべきであると小野寺は感じています。
なお、カオス結合系モデルにおいては、「アトラクタ」とよばれる一定期間、持続して維持される(ある特定の機能を発現する)秩序状態から、「急に出現する新しい状況」などの「外乱」によって、無秩序な(なんの機能も発揮しない)状態に一定期間、陥り、その後しばらくして、再び新しい(別の、あらたな状況に対応する機能を発揮する)「アトラクタ」とよばれる秩序状態へと、勝手に(自律的に)移行する、という「秩序相」と「無秩相」の間を時系列的に往還するダイナミクスを発生させます。
国吉・新山研究室が開発した運動・神経系の自己形成モデルや自己身体表象の獲得モデルも、このようなダイナミクスがきれいに現れたモデルであり、個々の「秩序相」が、そのときどきに遭遇している問題状況にうまく対応した能力を発揮している「状態」に対応するものです。
迷路のゴールに至る最短経路問題におけるカオス理論の適用例
強化学習や深層強化学習は、与えられた迷路について、スタート地点からゴール地点に至る最短経路を自力で発見する能力を示したことで、その有効性が確認されています。
では、この迷路問題を解くという課題に関して、カオス理論を用いたモデルは、どれくらい問題解決能力を発揮するのでしょうか?
ところで、自然界が生み出した粘菌が、その生物的な特徴能力を生かして、最短経路を見出すことができることが知られています
粘菌が「最短経路」を発見するに至る過程を、数理モデルとして表現したアルゴリズムのことを、「粘菌アルゴリズム」と呼びます。これは一種の迷路問題を解くアルゴリズムです。
カオス理論は、この「粘菌アルゴリズム」の数理モデルとして活用されている、というよりも、生物としての「粘菌」の細胞機能が、どのようにして発現しているのか数理モデルとして表現することで理解使用とする研究の中で、活用されているようです。
また、迷路のスタート地点からゴール地点に至る最短経路を探索する問題とは、やや趣が異なりますが、決められた複数の地点を、どの地点も2度以上、重複して訪れることなく、すべての地点を通過する経路を探索する課題である「巡回セールスマン問題」を、カオス理論を用いた非線形数理モデルで考究している研究も行われています。
以下に、これらの領域における論文の一例を掲げます。
- 小林 正樹 「細胞の自己組織化過程を光子でとらえる -細胞性粘菌の生物フォトン光子統計特性分析-」
- 小畠 陽之助 & 松本 健司 「アメーバ様運動細胞における運動リズムと知覚機能(生体 系,カオスとその周辺,研究会報告)」
- 矢野 雅文 「真性粘菌における情報の階層性とその統合様式(基研 長期研究会「カオスとその周辺」,研究会報告)」
- Haruna Matsushita & Yoshifumi Nishio, CHAOSOM and its Application to Traveling Salesman Problem
- 吉田 泰之ほか「カオスノイズを都市配置に加えた巡回セールスマン問題の解法」
- 狩野 修男「電流モードカオスニューラルネットワーク回路の設計とその巡回セールスマン問題への適用」
- 光岡 高宏 & 長谷川 幹雄 「Lin-Kernighan法をカオスダイナミクスで駆動する巡回セールスマン問題の解法とその性能について (非線形問題)」
- 手老 篤史「粘菌の輸送ネットワークから都市構造の設計理論を構築―都市間を結ぶ最適な道路・鉄道網の法則確立に期待―」
- 青野 真士 「真性粘菌アメーバの時空間振動ダイナミクスによる自己組織的計算」
- 小林 亮 「粘菌の経路探索における最適化」
- 横山 優希 「粘菌アルゴリズムによる最短経路問題の解法」
- 川上 聡治郎 「最短経路問題における粘菌アルゴリズムの数値実験」
- 伊藤 賢太郎 & 中垣 俊之「粘菌ネットワークの賢さ」
- 手老 篤史ほか「生物に学ぶ最短経路探索アルゴリズム(生命リズムと振動子ネットワーク)」
- 白田 勉「最短経路問題に対する粘菌アルゴリズムの収束性」
- 中垣 俊之 「脳や神経を持たない粘菌の情報処理能力を探る」
国吉・新山研究室で進行中の研究領域
ここで、東京大学の国吉・新山研究室が具体的にどのような「成長フェーズ」や「機能」を担うAIモデルを開発してきたのでしょうか。
また、それらの特定の「機能」を発揮する個々のAIモデルは、すでに到達済みの前段階の「成長フェーズ」を足場としながら、時系列過程として、どのような軌跡を辿りながら、自然発生的・自己組織化的に(連続的に)発生・出現してくることが、シミュレーションの結果として、得られているのでしょうか。
次に、これらの疑問について、同研究室のウェブページを頼りに、俯瞰的に眺めてみます。
なお、国吉 康夫教授は、東京大学・次世代知能科学研究センターのセンター長を兼任されています。
国吉・新山研究室の研究テーマ
同研究室の研究活動内容を紹介するウェブページ(http://www.isi.imi.i.u-tokyo.ac.jp/portfolio/all/?lang=ja)では、同研究室が以下の研究領域に重点的に取り組んでいることが、色鮮やかな画像写真をちりばめた魅力あふれるページ構成で、掲載・紹介されています。
上記のうち、「感覚・運動の発達モデル」に着目すると、以下の説明(部分のみ抜粋)が付されたいくつかのサブ・カテゴリが展開されています。
掲載されている日本語の説明文は、もとは英文であった(英文論文等の)文章を、コンピュータを用いて日本語に機械翻訳(自動翻訳)して生成した文であるのかどうかはわかりませんが、一部、翻訳調のいいまわしもありますが、そのまま抜粋して引用します。
・「身体性に基づく自発運動の創発」
→ 「(前略)この研究では、全身の筋を神経系レベルでは独立に制御しても、身体を通じて筋がお互いに影響を及ぼしあい、身体を通じてカップリングすることで、身体性に基づく自発運動が創発可能であることを示した」
・「身体構造が導く神経系・運動発達」
→ 「胚や胎児期の初期発達において、身体はどのような役割があるだのだろうか。(中略)共通のなる身体構造によって種固有の運動・神経系発達を実現し、(後略)」
・「子宮内触覚経験に基づく胎児の運動発達」
→ 「ヒトの(中略)触覚分布が、自発運動を通じた子宮内触覚経験に基づいた脊椎神経回路の自己組織化により、手と顔の接触運動や独立四肢運動といっり(ママ)観察される実際の胎児行動の一部、及びその順序性を再現可能でした(ママ)。」
・「自発運動を通じた身体表象の獲得と運動発達」
→ 「自分自身の姿勢や触覚情報は皮質において統合され、身体の各部に対応する脳内地図を構成することで身体表象が行われている。胎児シミュレータを用い、こうした皮質の身体表象の獲得において胎内環境における自発運動が重要であることを、構成論的に示している。更にこうした身体認知が胎児や乳児に典型的に見られる運動発達を可能にすることを示唆している。」
非周期な軌跡を辿る挙動のモデル化に力を発揮するカオス理論
カオス理論(複雑系科学)による数理モデルは、感覚需要刺激や運動動作が非周期的な時系列変容をたどりながら、軌跡が一定の軌道の範囲内に収束する期間(「アトラクタ」に引き込まれている期間)から、ランダムな無秩序な軌道を経て、再び、今度は別の一定の軌道の範囲内に収束する期間(「アトラクタ」に引き込まれている期間)に至る時系列過程を辿る挙動をシミュレーションするのに有効です。
このあたりについて、国吉教授は、ロボットによる人間の動作の「模倣」というタスクとも絡めて、日経サイエンスの2004年1月号「特集:ロボットから人間を読み解く機械はコツを身につけられるか」で次のように述べています。
この記事は、当時、東京大学助教授であった国吉教授が開発した「寝そべっていた状態から両脚を上げ,振り下ろす反動で起き上がる」動作をなめらかにとることができる「ヒューマノイド(人間型ロボット)」・「Rダニール(R-Daneel)」の公開実験を行ったのを受けて行われたインタビュー記事です。
そこで国吉助教授(当時)は、ある動作(動作の軌跡の軌道がある収束点のまわりを安定的に、一定の軌道のずれを伴いながら周回する秩序状態)から、無秩序な過程を経て、再び別の動作(軌跡軌道の周回現象)へと遷移する挙動をカオス数理モデルでモデル化することについて、次のように述べています。
起き上がりのように,線形方程式では表せない,異なった複数の動作が次々に現れるような運動や周期的でない運動にはどう対処するのか。また,複数の動作の境目はどのように決まり,どう制御すればよいのだろうか。私たちはこんな問題意識で研究を進めている
(中略)
人間の起きあがり動作を調べると面白い現象が見つかった。動きの軌道がある局面ではいつも同じ位置に重なって収束し,別のところでは毎回バラバラだったことだ。ポイントを押さえ,そこさえきちんと制御すればよいことになる。これが「コツ」と呼ばれるものに相当するのではないかと考えている。ダニールは起きあがり動作のコツを習得させて実践した。
コツは運動だけでなく,自分や他人の行為を認識するうえでも重要な意味を持つ。行為のところどころに現れる「目のつけどころ」に集中して情報処理をし,ほかの部分は分節点の位置を決めるためだけに“軽く流して”処理すればよい。因果関係や文脈に基づいた事象予測を手がかりに行為の分節点を検出し,そこで重点的に行為識別情報を抽出することができれば,ロボットに見まねをさせられる。
周期運動のモデル化は、「神経振動子」を用いた松岡モデル等が有名
その一方で、感覚刺激や運動動作が、周期的な軌跡(ある種のリズム運動と呼べる動き)を辿る挙動を数理モデル化する試みとしては、自然界に存在する生物の骨髄に存在するとされる、周期運動を生み出す「神経振動子」(CPG: Central Pattern Generator)が知られています。
この「神経振動子(CPG)」を数理モデル化したものとして、制御工学分野でしばしば使われるものとしては、松岡モデル(K.Matsuoka (1985), Sustained oscillations generate4d by mutual inhibiting neurons with adaptation)があります。
この松岡モデルを、二足歩行や四脚歩行を行うロボットの各脚に埋め込んで、自然な歩行動作(歩容)を再現する機械シミュレーションに成功した研究事例としては、一例として、以下の論文があります。
- [名古屋大学] 野田ほか, 「神経振動子を用いたラットの歩行シミュレーション」, 2011年 第54回自動制御連合講演会
- [東京理科大学・埼玉大学] 丸山ほか, 「人とロボットの歩行同期に向けた神経振動子の視覚刺激への引き込みシミュレーション」
この他、「神経振動子(CPG)」を用いて制御系モデルの研究に取り組んでいる研究室としては、例えば、山口大学の生体情報システム研究室による「身体と神経系の相互引き込みによる学習制御理論」等があります。


























