この記事では、機械学習をこれから勉強するうえで数学に対してどのように向き合っていけばいいのかについて解説します。
初学者や特に人文学系など理系科目を専門にしていない人たちにとって、どうしても数学には難しい、取っつきにくいというイメージがつきものだと思います。
この記事では、機械学習に必要な数学のロードマップや勉強法について紹介します。少しでも勉強の助けになれば幸いです。
目次
機械学習と数学の関係
機械学習と数学は切っても切り離せない関係にあります。本節では、機械学習と数学の関係について紹介します。
機械学習において数学を学ぶべき理由
機械学習を理解するためには、数学の知識が必須です。機械学習のアイデアは数学上の発見に由来するものが多く、数学とコンピュータ・サイエンスは相互に影響を与えながら発展してきました。
しかし、機械学習の理解のために数学の知識が必要だからと言って、「すべての機械学習を扱う人が数学を勉強しなけばならない」というわけではありません。この点については次節でもう少し詳しく解説します。
コンピュータと数学の歴史
機械学習と数学の密接な関係を歴史の観点からみていきましょう。

出典:https://commons.wikimedia.org/wiki/File:Boulier1.JPG
コンピュータを日本語に訳すと計算機となります。計算機のアイデア自体はかなり昔からあり、世界中に日本の「そろばん」のような計算機は点在しています。

出典:https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Leibnitzrechenmaschine.jpg
機械式計算機としてのコンピュータのアイデアは、17世紀の数学者ブレーズ・パスカルやゴッドフリート・ライプニッツが考えていました。ちなみに、ライプニッツは2進法の考案者でもあります。
これらの計算機はまだプログラムが搭載されていませんが、自動で簡単な計算を行うことができます。
「計算可能性」の発見
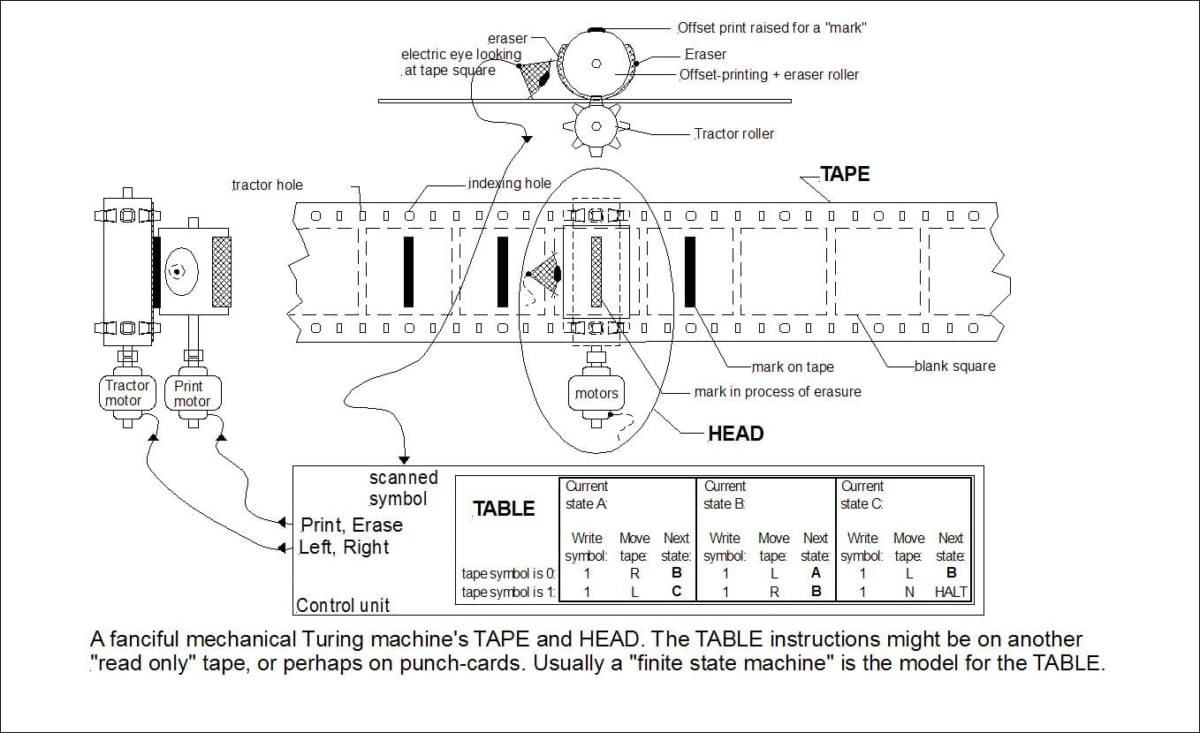
出典:https://en.wikipedia.org/wiki/Turing_machine_gallery
私たちが普段使っているようなコンピュータは20世紀初頭に発明されました。数学者チューリングは、チューリングマシンという抽象機械を考案し、プログラムにしたがってハードウェアとソフトウェアが動作を実行します。
チューリングマシンは、計算可能性という概念を説明するために考案されました。これによって計算が厳密に定義されました。
機械学習と数学の歴史

出典:https://sites.google.com/site/generaciondelascomputadorase3/home/our-story-2
数学者フォン・ノイマンは、チューリングマシンのアイデアを受けて、大量の真空管とケーブルからなる機械としてのコンピュータを実現しました。このコンピュータをノイマン型コンピュータといい、現代のコンピュータのほとんどはこのノイマン型コンピュータの方式を採用しています。
チェッカー・プログラム

ノイマンによって、コンピュータは膨大な計算能力を手に入れました。アーサー・サミュエルは、日進月歩で増大していくコンピュータの計算能力をうけて、機械学習のアイデアを考案しました。
彼は、チェスの問題を解かせるチェッカー・プログラムを開発し、これは世界初の学習プログラムだといわれています。この時代は、AIの歴史でいうところの第1次AIブームに該当します。この第1次AIブームを受けて機械学習の研究が盛んになり、いくつかのブレイクスルーを経て現在に至ります。
▼AIの歴史について詳しくはこちら
機械学習において数学を学ぶ際のポイント

具体的な数学分野の話に移る前に、機械学習のための数学を勉強する際のポイントについて紹介します。
機械学習に数学は必要?
そもそも、あなたにとって数学の勉強が不要である可能性もあります。
大抵の機械学習ライブラリは、数学の知識なしで動かすことができるような仕組みになっています。そのため、機械学習をツールとして使い簡単な分類や推測を計算したい人にとって、数学の勉強は割に合わない努力に終わってしまうこともあり得るのです。
もちろん、勉強して無駄なことはありませんが、機械学習ライブラリのテンプレート機能は非常に優秀なので、人によっては無理して数学を学ぶ必要はないでしょう。
数学やプログラミング不要のAI技術活用サービス

出典:https://www.matrixflow.net/
例えば、株式会社「MatrixFlow」は、数学やプログラミング、機械学習の専門的な知識なしでAIを活用するためのプラットフォームを開発しています。
これからも機械学習ライブラリが発展するにつれて、ユーザー側が数学知識なしでも、さまざまなことができるようになるでしょう。
機械学習の結果をより深く理解するためには、数学知識が必須
先程、「人によっては無理して数学を学ぶ必要はない」と述べましたが、機械学習の結果に対して、「なぜこの結果になっているのか」や「さらに結果をよくするためにはどうすればいいのか」といった問題を考える際には数学知識が必須です。
実際、簡単な機械学習をするだけでは得られるものは多くありません。何度も何度も試行錯誤をしながら計算値をより深くまで掘り下げることによって、機械学習の恩恵を十分に得ることができます。
深層学習はより複雑な数学を必要とする
ディープラーニング技術の登場は、第3次AIブームのきっかけになりました。ディープラーニングは、従来の機械学習よりもはるかに大きなデータ群を扱える一方で、内部的により複雑な計算を行っています。
ディープラーニングは高度な技術であり、これを扱うためには数学の知識があることが好ましいと言えます。基本的な機械学習に加えてディープラーニングを扱う人であれば、より高度な数学の勉強に取り組んでみることをおすすめします。
機械学習にはどのような数学が必要なのか
この章では、機械学習において学習するべき数学分野を一気に列挙します。
読者のなかには「これをすべて勉強しないといけないのか…」と困惑する方もいるでしょう。すべてを一気に勉強しようとすると大変で疲れてしまうので、自分が本当に必要な分野を見極めて勉強することが大切です。
それでは、機械学習を学ぶ上で必要な数学の分野について簡単に解説します。
中学・高校数学までの内容
機械学習における数学を理解するためには、中学・高校で習うような数学の知識が必須です。
中学・高校数学をしっかりと理解することで、機械学習がどのような過程を経て動いているのか、どのようなアイデアに基づいているのかを部分的に理解することができます。
中学・高校数学の知識を固めたら、次は大学数学の勉強へと移りましょう。大学数学の分野では、大きく分けて線形代数、確率・統計、解析学(微分積分)の3つが基本になります。
線形代数 / 確率・統計 / 解析学(微分積分)
一般的な理系の大学では、1・2年生の一般教養科目として線形代数と微分積分を学びます。
線形代数
高校では主に幾何ベクトルを学びますが、大学数学ではより抽象化した線形空間やベクトル空間を扱い、その様々な演算を学びます。
機械学習分野と線形代数は密接に関係しています。コンピュータがどのようにしてデータを扱っているのか、コンピュータが機械学習におけるパラメータの最適化をどのようにしているのかを理解する上では、行列計算の知識が欠かせません。
解析学(微分積分)
微分は局所的な変化を扱う学問で、積分はその変化を積み重ねた量を扱う学問です。高校数学の微分・積分は、変数が少なく限られた条件下での計算でしたが、機械学習はより複雑な計算を扱います。
確率・統計
機械学習を理解する上では、確率・統計の知識が欠かせません。機械学習の技術的な目標は、大量のデータを学習して予測値と実際の値の誤差を少なくすることです。確率・統計を勉強することで、そのプロセスを理論的に理解することができます。
その他・発展的内容
機械学習に限った内容ではありませんが、一般的にIT分野やプログラミングを理解するために必要だとされている数学分野を紹介します。
「アルゴリズムとデータ構造」という分野は、コンピュータが内部で処理しているプロセスを数学的に説明する学問です。特に競技プログラミングをやっている方には馴染みがある分野なのではないでしょうか。これをもう少し一般化した数学分野が「離散数学」や「グラフ理論」です。
前節で、コンピュータの理論はもとをたどれば集合論や論理学に行きつくことを紹介しました。
このあたりのことを理解するためには、「論理回路」や「形式言語とオートマトン」、「代数学」の知識が必要です。コンピュータを根本的に理解したい人は、これらの分野の学習をおすすめします。
機械学習における数学の勉強方法
それでは、機械学習における数学のおすすめの勉強方法を紹介していきます。自分にあった勉強方法を見つけて集中的に勉強するのもいいですし、さまざまなアプローチで多角的に数学を勉強するのも良いでしょう。
本で学ぶ
1つ目は本で学ぶという方法です。
本は情報の正確さや豊富さに優れています。また、自分の知識にあわせて本の難しさを選ぶこともできます。初心者向けの本は、難しい定義や数式を図やイラストを用いてわかりやすく説明されているものが多く、上級者向けの本は、詳細なことまで丁寧な説明がされていて、より数学の本質に迫る内容になっています。
本の中でも特におすすめなのが、次の6冊です。
フェルマーの最終定理

出典:https://www.shinchosha.co.jp/book/215971/
数学の勉強をするためには、「数学の勉強が好きになること」がなにより重要です。そこで、まず数学の勉強を好きになることにうってつけの本、サイモン・シン著『フェルマーの最終定理』を紹介します。
本書は、数学における最大の未解決問題といわれたフェルマーの最終定理をめぐる数学者たちのドラマが描かれているノンフィクション作品です。
数学への興味が駆り立てられる魅力的な作品なので、これから本格的に数学の勉強をはじめようとする人におすすめの一冊です。
人工知能プログラミングのための数学がわかる本

出典:https://www.kadokawa.co.jp/product/321708000339/
「この1冊で人工知能の数学がゼロからわかる!」と書かれた表紙の通り、この1冊だけで人工知能プログラミングに必要な中学・高校数学、大学数学を勉強することができます。
本書の後半では、pythonコードが書かれており、それを動かしてみることで、実際の人工知能の機械学習プロセスを勉強することもできます。基礎から応用まで幅広く扱う定番の1冊です。
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装

出典:https://www.oreilly.co.jp/books/9784873117584/
この本は機械学習や、より複雑なディープラーニングに必要な数学の知識を簡単に説明しています。どのような数式を用いて機械学習やディープラーニングのプロセスが動いているのかを実際にコードを書きながら勉強することができます。
上述の2冊は機械学習に必要な数学の知識にフォーカスした本ですが、次の3冊をきっかけに数学を専門的に勉強することによって、より深い知識を得ることが可能です。
チャート式シリーズ大学教養 線形代数

出典:https://www.chart.co.jp/goods/item/sugaku/44006.php
高校数学の定番の参考書であるチャート式シリーズが2020年に出版した線形代数の参考書です。チャート式特有の問題演習中心の参考書で、この本を一歩一歩勉強していくことで着実に線形代数の知識が身についていきます。
チャート式シリーズ大学教養 微分積分

出典:https://www.chart.co.jp/goods/item/sugaku/39952.php
こちらは青チャートの微分積分です。導入部分で高校数学と大学数学の橋渡しが丁寧になされています。豊富な問題と丁寧な解説が載っているので、たくさん計算をこなすための問題集として利用することができます。
プログラミングのための確率統計

出典:https://www.ohmsha.co.jp/book/9784274067754/
機械学習だけでなく、「プログラマー」と呼ばれる人たちが取り組む問題には確率統計の知識は欠かせません。決して易しい内容ではありませんが、丁寧な解説とプログラミングの視点からの補足説明で確率統計の知識を深めることができます。
本書は、基礎的な内容だけにとどまらず、確率統計の定義の本質にまで迫ろうとする良書です。
ネット講座で学ぶ
2つ目はネット講座で学ぶという方法です。
勉強のペース配分を定めてコツコツ勉強したい人、いきなり本を読むのはハードルが高いと考える人におすすめです。ネット講座は無料のコンテンツだけでなく、有名講師の授業や個人指導などのサービスがついてくる有料のコンテンツが豊富にそろっています。
ネット講座の中でも特におすすめなのが、以下の3つです。
AIのための数学講座(Udemy)
 Udemyは、世界中で5,000万人が利用するオンライン学習プラットフォームで、15万以上の講座が公開されています。
Udemyは、世界中で5,000万人が利用するオンライン学習プラットフォームで、15万以上の講座が公開されています。
Udemy講座の中でも特におすすめなのが、「AIのための数学講座(有料)」です。同講座では、プログラミングの知識を前提にせず、中学数学程度の知識から丁寧に解説しており、AIの勉強に必要な数学の知識が動画を通じてわかりやすく解説されています。
ほかにもUdemyには機械学習に関連した講座が充実しているため、気になる方は調べてみるといいでしょう。
Chainer チュートリアル
出典:https://tutorials.chainer.org/ja/tutorial.html
無料のネット講座の中でも、特におすすめできるのが「Chainer チュートリアル」です。
Chainer チュートリアルでは、機械学習に必要な数学の知識を一通り見通すことができます。
Chainer チュートリアルの強みは、数学講座で学んだことをその後のセクションでpythonライブラリの勉強をしながら実装できる点です。
また、数学の勉強をしながらデータ分析やディープラーニングの実践的なスキルを身に着けられるのもChainer チュートリアルの大きな魅力だと言えます。
キカガク (KIKAGAKU)

出典:https://www.kikagaku.ai/
キカガクは、AIや機械学習のネット講座で有名なサービスです。この講座は数学に特化した講座ではありませんが、数学も含めて機械学習全般の知識をプロの講師がわかりやすく説明してくれています。
キカガクの特徴は、たくさんの企業がクライアントやパートナーとして参加していることで、多くの企業の人材育成に活用されています。
youtube動画で学ぶ
3つ目はyoutube動画で学ぶことです。
最近は、さまざまな分野の専門家たちがyoutubeチャンネルを解説して、数多くの動画をあげています。youtubeが学習ツールの定番になる日もそう遠くないかもしれません。
【9分で分かる】AI・機械学習の勉強に必要な数学の基礎を徹底解説!微積分・線形代数・確率統計
この動画は、機械学習の勉強に必要な数学知識を微積分、線形代数、確率統計の3つのパートに分けてわかりやすく解説しています。要点が短くまとまっているため、おすすめです。
中学数学からはじめるAI(人工知能)のための数学入門
この動画は、特にAIをプログラミングする際に必要な数学の知識を解説しています。中学数学からわかりやすく丁寧に解説されているため、特に数学に苦手意識を持っている方におすすめです。
また、この動画を投稿したチャンネルであるヨビノリのホームページでは、おすすめの参考書が紹介されています。他の動画と合わせてこちらも参考にしてみるといいでしょう。
大学のオンライン講座で学ぶ
大学の講座のなかでは、一般に無料で公開されているものもあります。基礎的な内容から非常に発展的な内容まで、幅広くそろっています。
大学のオンライン講座の中でも特におすすめなのが、以下の3つです。
筑波大学オープンコースウェア

出典:https://ocw.tsukuba.ac.jp/course/systeminformation/machine_learning/
筑波大学オープンコースウェアは、筑波大学で開催されている授業の内容をそのまま一般に公開しているサービスです。
特におすすめな講座は、佐久間淳教授の機械学習講座です。この講座では、機械学習の理解に必要な発展的な数学を解説しています。実際に大学で行われている講義に無料でアクセスできるため、おすすめです。
Deep Learning基礎講座演習コンテンツ
出典:https://weblab.t.u-tokyo.ac.jp/deep-learning%E5%9F%BA%E7%A4%8E%E8%AC%9B%E5%BA%A7%E6%BC%94%E7%BF%92%E3%82%B3%E3%83%B3%E3%83%86%E3%83%B3%E3%83%84-%E5%85%AC%E9%96%8B%E3%83%9A%E3%83%BC%E3%82%B8/
東京大学の松尾研究室が開発している学習コンテンツです。機械学習のなかでもディープラーニングに特化しています。
Courseraの機械学習講座

出典:https://www.coursera.org/learn/machine-learning
多くの海外の大学の機械学習講座がcourseraで公開されています。特に有名なものは、Stanford大学のAndrew Ng講師の講座です。機械学習の基礎から応用まで、数学とプログラミングの両方の観点から詳細な講義を受けることができます。
おわりに
ここまで、機械学習における数学の勉強方法について紹介してきました。機械学習を理解するためにはかなり広範な数学の知識が必要になり、一筋縄ではいかないことも多いでしょう。
大切なことは、勉強を継続させるために無理をしないこと、適切な目標をたてて着々と課題をこなしていくことです。この記事が自分にあった勉強方法や目標を見つける参考になれば幸いです。