みなさんMLP(多層パーセプトロン)をご存じでしょうか?機械学習を使って何か開発してみたいと思っている人の中には、MLPっていったい何だろうと思っている方もいるでしょう。AIについて興味がある人にとってMLPの知識は持っていて損はないものです!そこで今回は機械学習におけるMLPについて詳しくご紹介したいと思います!
目次
MLP(多層パーセプトロン)とは
MLP(多層パーセプトロン)とは人間の脳をモデル化したパーセプトロンというものを多層化したもののことです。これは、機械学習のアルゴリズムの1つであるニューラルネットワークの基本となるものです。
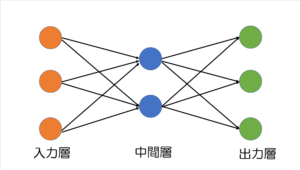
単純パーセプトロンは入力層と出力層からなるのに対し、上の図のようにMLPには入力層・中間層(隠れ層)・出力層の最低でも3つの層からなり、層が複数追加されているのが特徴です。
他のニューロンで出力されたものを別のニューロンの入力に使えるので、単純パーセプトロンで行われる計算を多層パーセプトロンでは一度に複数行えます。現在の機械学習の多くにはこの多層パーセプトロンの形式を拡張したものが使われています。
MLPにできる3つのこと
MLPには主に3つのことができます。
いろいろなデータを機械学習できる
このMLPの学習には誤差逆伝播いろいろなデータを機械学習できる法が用いられています。これは、入力データ(判断材料)に重み(どのデータをどのくらい重視するか)を設定し、出力データと学習データとの間の生じる重みの誤差が最小になるように増減して調節することです。これにより、全ての重みを学習していろいろなデータをうまく分類することが可能になるため、さまざまなデータに対して機械学習ができます。
未知のデータを予測できる
MLPは回帰問題を推論できます。回帰問題とは連続した数値に基づくデータを予測することです。「AがわかるとBが予測できる」というように今までのデータから別のデータを予測できます。例えば、過去の売上のデータから来年の売上の予測が可能です。
線形分離不可能な問題が解ける
「線形分離不可能」とはX軸・Y軸上の平面に分布するデータを1本の直線で分類できないことを言います。
MLPは先ほど述べたように複数の中間層が追加されたものですので、複数のクラス分類が可能です。単純パーセプトロンでは平面を直線的に処理することしかできなかったのですが、多層パーセプトロンでは平面を曲線的に分類することが可能になるという利点があります。複雑な問題処理が必要な機械学習において欠かせないものであることがわかりますね。
MLP・機械学習・ディープラーニングの関係性とは
ではMLPは機械学習やディープラーニングとどのような関係なのでしょうか。機械学習におけるMLPがどのようなものなのかくわしく紹介します。
MLPと機械学習・ディープラーニングとの関係
次にMLPと機械学習やディープラーニングとの関係性について説明します。
そもそもディープラーニングは多数のデータから解を導きます。ディープラーニングもMLPもニューラルネットワークを発展させた機械学習手法の1つで、人工のニューラルネットワークは人間の脳のネットワークを模倣したものですが、その人工ニューラルネットワークが発展するなかでMLPの構造が用いられるようになりました。
もともとは単純パーセプトロンしか存在しませんでしたが、その欠点を埋める目的でMLPが誕生しました。MLPはディープラーニングを模した構造をとっています。
機械学習・ディープラーニングについて詳しく知りたい方はこちら
MLPとCNNの違いとは?
MLPに似たものにCNN(畳み込みニューラルネットワーク)というものがあります。以下ではMLPとCNNの違いについてご紹介します。
MLP
MLPとは、入力層と中間層と出力層のニューロンが全部結合されている一般的なニューラルネットワークです。MLPでは出力に関係のないデータも他のニューロンに軽都合します。
CNN
CNNは畳み込みニューラルネットワークとも呼ばれます。MLPが全結合であるのに対し、ニューロン同士の結合を出力に必要なもののみに制限しています。また、「重み共有」できるのも特徴です。
CNNについて「詳しく知りたい方はこちら
▶︎CNN(畳み込みネットワーク)とは?図や事例を用いながら分かりやすく解説! | AI専門ニュースメディア AINOW>>
機械学習に使われるPythonとは?
Pythonとは機械学習を用いたAIの開発に使われるプログラミング言語です。Pythonはさまざまな企業でも用いられるほど一般的です。例えばYouTubeやinstagramでもPythonが用いられていることで有名です。Pythonはこのように信頼性が高いことや文法の簡潔さから人気の高いプログラミング言語です。
実際にMLPの実装をする際にはPythonを用いることをおすすめします。
Pythonについて詳しく知りたい方はこちら
▶︎《初心者向け》機械学習をPythonで学ぼう|できることやライブラリも紹介 | AI専門ニュースメディア AINOW>>
MLPを応用したニューラルネットワークを紹介
MLPを応用して、より効率的にデータを出力できるニューラルネットワークがたくさん生まれています。以下で4つのニューラルネットワークをご紹介します。
CNN(畳み込みニューラルネット)
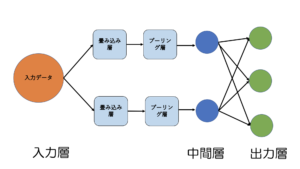
CNN(畳み込みニューラルネット)は入力層と中間層の間に畳み込み層とプーリング層というものが差し込まれたものです。
RNN(再帰型ニューラルネット)
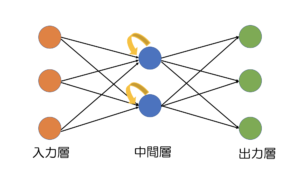
RNN(再帰型ニューラルネット)は中に循環を持つニューラルネットワークです。MLPではできなかった時系列データの予測をする際に利用されます。ある時点での出力データが他のネットワークの入力に利用できる構造です。
LSTM(長短期記憶)
LSTM(長短期記憶)とはRNNの一種で、時系列データの学習に長けているという特徴があります。
ネットワークの短期記憶を長期間記憶・活用できます。RNNではデータが離れれば離れるほど他の関連する入力に繋げることが難しくなりますが、LSTMでは関連データが離れていても繋げることが可能です。
GAN(敵対的生成ネットワーク)
GAN(敵対的生成ネットワーク)とはデータから特徴を学習し、新しいデータを生成することができるものです。GANは生成ネットワークと識別ネットワークから構成されており、それらを競わせることで学習できます。
これを利用することで、複数の画像データから別の画像データを生成したり、ピンボケした画像を綺麗な画像に変換できます。
MLPの実装方法
では実際にMLPを実装してみましょう
XORとは
XORとは排他的論理和とも言います。2つのうち1つだけ正しければOK、両方正しいまたは両方間違っていたらNGという論理演算のことです。
簡単にいうと
|
このような結果を示す演算のことです。
実装
実装の方法をおおまかに8つのステップで紹介します。
ステップ1:ネットワーククラスを作る
ステップ2:重みを初期化する
ステップ3:データセットを取り込む
ステップ4:形式ニューロンの実装
ステップ5:順伝播処理を実装する
ステップ6:学習部の実装
ステップ7:重みの更新式を実装し終了条件を決定する
ステップ8:テスト部を実装する
これらを進める中で逐一動作確認を行うと良いです。
実装方法はこちらの記事を参考にしてください
MLPの動向と将来性
これから人工知能を用いたAIが発展していく中で、幅広く応用の効くMLPがより多くのデータ学習をサポートすることが期待されています。
MLPは基本的なニューラルネットワークですが、紹介したように応用されたニューラルネットワークがたくさん開発されています。将来的にはより複雑な機械学習にMLPやMLPが応用されたニューラルネットワークが活用されるでしょう。
まとめ
いかがでしたか。今回はMLPについてできることから応用、実装まで紹介しました。
機械学習においてMLPなどのニューラルネットワークの構造に興味を持った方はこれをきっかけにMLPをはじめとしたニューラルネットワークについて勉強してみてはいかがでしょうか。
最後までご覧いただきありがとうございました。