決定木
決定木とは
データをもとに、図のような樹木状のモデルを作成し、意思決定をする手法。木は簡潔でわかりやすいため、様々な応用に用いられます。 パターン認識 の分野でも木構造は重要なモデルで、分類や回帰に用いられる木は決定木と呼ばれます。特に分類で用いられる決定木を分類木、回帰で用いられる決定木を回帰木と呼びます。決定木は、クラスや目的関数の予測だけでなく、重要な属性やその値の範囲などを解析するためにも役立ちます。
分類木と回帰木
特徴ベクトルをx=(1,x₁,・・・,xd)T=(1,xT)T及び目的変数yについて考えます。
もし目的変数yがクラスを表すなら分類問題、目的変数yが実数であれば回帰問題となります。
まず分類問題から考えていきましょう。
次の図に、d=2のデータの例を挙げました。
横軸に特徴量x₁、縦軸に特徴量x₂を取っています。
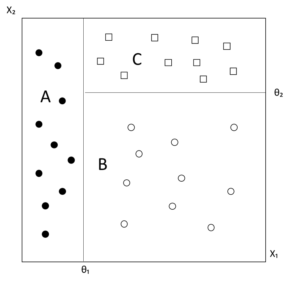
出典)後藤正幸、小林学 「入門 パターン認識と機械学習」 コロナ社p73を参考に作成
このデータを見て見ると、
x₁<θ₁ →クラスA
x₁≧θ₁かつx₂<θ₂ →クラスB
上記以外のデータ →クラスC
というように分けられています。
このように特徴量の大小によってデータのクラスを決める場合には分類木を用いるのが有効です。
下の図は上記のデータを分類した分類木です。
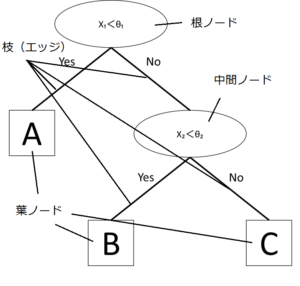
出典)後藤正幸、小林学 「入門 パターン認識と機械学習」 コロナ社p73を参考に作成
木構造に関する用語は、図の通りです。
ノードから下に直接枝で結ばれたノードを子ノードといい、その元のノードのことを子ノードから見て親ノードと呼びます。
この分類木では、あるデータに対してx₁<θ₁を満たす場合はYes、満たさない場合はNoをたどります。ここでYesをたどった場合、このデータはクラスAに分類されます。また、Noをたどった場合はx₂<θ₂のノードにたどり着き、またこの条件に対してYesかNoか判定します。このときYesをたどるとクラスBに、NoをたどるとクラスCに分類されることになります。
このように、分類木では根ノードから始まり、中間ノードで特徴量の大小で分岐、葉ノードでクラス分けを行います。
次に回帰木について考えます。
この回帰木と分類木の違いは、葉ノードのラベルのみです。
分類木における出力はクラスでしたが、回帰木における出力は目的変数yの具体的な数値の予測値になります。ですから、回帰木の葉ノードには目的変数の推定値が入ります。
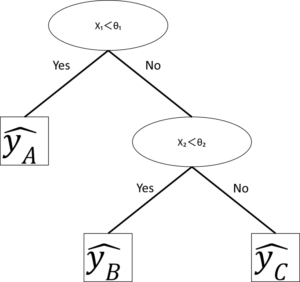
出典)後藤正幸、小林学 「入門 パターン認識と機械学習」 コロナ社p73を参考に作成
このように、決定木を使うことで入力されたデータを素早く分類または回帰を行うことができます。