最終更新日:

目次
論文:Ricky T. Q. Chenほか(2018)Neural Ordinary Differential Equations
今年(2018年)も残すところあと1週間です。
今年を振り返る方法には各人各様の方法があると思いますが、僕は少し背伸びして(そして気取って)、情報処理と人工知能の学術分野で最高峰レベルの国際論文誌であるNIPS(Neural Information Processing Systems)で採択された論文を振り返ってみました。
(なお、NIPSは正式名称は変わらないものの、略称はNIPSではなく、NeurIPSに変わったようです。しかし、まだNIPSという略語が研究界隈では定着していると思いますので、この記事ではこれまでのNIPSという略称を使いたいと思います)
膨大な数の論文がありますが、NIPSで今年、最優秀論文の栄光に輝いた以下の論文をチェックしてみたところ、その栄光に輝いたのは、またしてもカナダのトロント大学に所属する研究陣でした。
トロント大学は、「ニューラル・ネットワークの冬の時代」に終止符をうち、今日のディープ・ラーニングブームを到来させたAIの巨人とも形容すべきヒントン教授を擁することで、その名を轟かせています。
そのトロント大学は、去年(2017年)も、Capsule Network(CapsNet)を世に打ち出すなど、小手先のモデル構造の改変ではなく、ニューラル・ネットワークモデルの構造の根本に新基軸を打ち出すインパクトの大きい論文を打ち出し続けていることで、その研究力の大きさを感じることができます。
そして、Capsule Networkに続く今年、またまた超ド級の論文が登場しました。しかも、NIPS最優秀論文賞に輝いています。トロント大学、恐るべし、と言わざるを得ません。
取り上げている記事
この論文を取り上げて解説している記事としては、以下のWired誌(オンライン版)が見当たりました。
この記事では、医療計測データの解析場面を例に挙げて、このモデルがこれまでのディープ・ラーニングモデルに比べて、どのような利点を秘めているのかを解説しています。
- MIT Technology Review(和訳版)「機械学習の『限界』を克服 – トップ学会で称賛された新設計のニューラル・ネット」
- 同上(英語原文記事)A radical new neural network design could overcome big challenges in AI
新基軸:中間層を離散的に並べた構造を卒業する
この論文を通じて、トロント大学が世に打ち出したのは、またしても、現在主流のニューラル・ネットワークモデルの基本構造を、根底から書き換えようとする新基軸の提案でした。
そこで提案されていたのは、入力(層)から出力(層)まで、至るところ微分可能な(数学的に)滑らかな連続な(高次元)空間で”つながった”ニューラル・ネットワークモデルでした。
そうです。複数の中間層が、互いに空間のすきま(間隔)を隔てて、入力層から出力層に方向付けられた1次元方向に、離散的に飛び飛びに配置された構造で居並ぶおなじみのニューラル・ネットワークのモデル構造ではないのです。
2018年現在、おびただしい種類の構造をもつ(多層)ニューラル・ネットワークモデルが提案されています。しかし、どのモデルも、隣り合う(任意の2つの)中間層どうしは、間に隙間があり、離散的に切り離されています。
このおなじみのニューラル・ネットワークモデルでは、データが順方向に受け渡されるときも、逆方向に流れるとき(出力層から出たモデル推計値と正解データとの「誤差」が、出力層側から入力層側へと偏微分演算をchain-ruleに基づきながらたどるとき)も、データは、隙間を挟んで離散的に並んだ隣り合う2つの中間層の間を行き来していました。
せいぜい、空間内に、中間層(内の各ノード)を配置する自由度としては、1次元方向に並ぶ構造から決別して、中間層を縦横斜め3次元方向に格子状に配置したGrid-LSTMモデルが、目を引く新しいモデルとして、一部で注目を集めた程度でした。
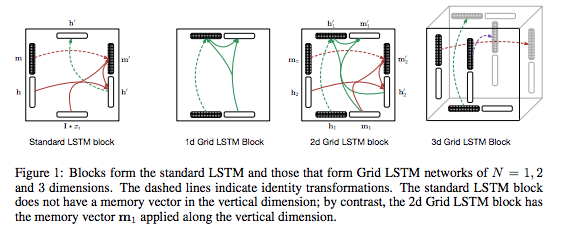
Grid-LSTM提案論文に掲載されているFigure.1
しかし、NIPS 2018の最優秀論文に輝いたトロント大学の論文は、これまでのニューラル・ネットワークモデルのモデル構造がもつ常識を、大きく乗り越えるものでした。
これは、ニューラル・ネットワークモデルに、(これまで誰も気づいていなかった)新たな可能性の息吹きを吹き込むものとして。受け止めることができるかもしれません。
なお、Wired誌の記者に対するインタビューの中で、至るところ微分可能な連続空間の構造を持つニューラル・ネットワークモデルの構想は、他の研究者がすでに考案済み(発見済み)のアイデアであり、この論文は、そのアイデアに具体的な形をいちはやく与えたものであるという証言が、論文執筆者のひとりによって、告白されています。
それでは、隣り合う中間層どうしを離散的に切り離さないで、微分可能な連続空間に結合することで、何が得られるのでしょうか?そして、トロント大学の研究チームは、今回なぜ、このような斬新なモデル構造を具備したニューラル・ネットワークモデルを提案したのでしょうか?
問題意識:不規則な時系列データに対応するために、中間層を離散的に並べた構造を卒業する
論文と、Wired誌とのインタビューの中で、これまでの中間層を離散的に飛び飛びに配置したニューラル・ネットワークモデルでは、以下のようなデータセットを入力値として受け取った場合、うまく対処できないということが、問題提起されています。
- 時系列データの欠損値に対応できない
- 入力データの時間間隔が不揃いな場合に対応できない
2で挙げられているのは、毎回、異なる時間間隔を置いて観測されたデータです。
そのようなデータ・セットの例として、論文中では、以下が挙げられています。
- (個人患者の)医療計測データ
- 通信ネットワーク上のトラフィック計測データ
- ニューロンの発火(スパイク)を観測したデータ
これらのデータは、IoTデータを情報処理する情報解析技術や、インターネットの通信空間の安全安心を監視するための情報処理技術が、私達の日々の暮らしを支えるインフラAIとして、日に日に不可欠な技術となりつつあるなかで、確かに、AIとして直面しているひとつの大きな限界であると受けとめることができます。
解決策:任意の2時点間のデータについて、パターン学習が可能な新モデルの提案
そこで提案されたのが、以下のような、時系列データについて、任意の2時点間のデータについて、その2時点間の時間間隔が、前後の他のデータの間に存在する時間間隔とは異なる”データ取得間隔が不揃いな”不規則データであっても、2つのデータの間のデータ構造(パターン構造)を学習し(順方向と逆方向、双方のデータ処理)モデルを推論することができる以下のようなモデルでした。
提案モデルの特徴:Neural Ordinary Differential Equationsモデル
上段のStateに描かれているのが、ある任意の時系列過程をたどる事象を、各時点(t0〜tN)で観測したデータ値の軌跡(trajectory)を描いた様子です。
ここで原論文から引用したFigure.2に描かれているように、このモデルは、入力データとして受け取った時系列データのうち、任意の2時点間の時系列過程に潜むパターン構造を学習できる(?)ようです(すいません、、まだ理解が生半可です。。)。
その理由は、次に見るように、このモデルは、従来のニューラル・ネットワークにおける「隣り合う2つの中間層の間」、に相当するところの「任意の2(時点)データ間」に生じる数値の変化を、2点間の値の変化率の極限値(平均変化率の微小変化量δ(デルタ)を限りなくゼロに近づけた値である微分値)を微分演算によって演算することで、数学的に求めることができるからです。
そして、ここで重要なのは、微分演算は「任意の距離によって隔てられた2点間」で求めることができることです。これが、このモデルが、データ間隔が不規則な時系列データを取り扱うことのできる仕組みである(理解が間違っていたらごめんなさい)ようです。
この仕組みにより、隣り合う中間層の間が空間で隔てられていて、中間層どうしの連結構造が非連続な飛び飛び(離散的な飛び地)であった従来の(多層)ニューラルでは、上手に取り扱うことができなかった、個々のデータ取得時点の間の時間間隔(time intervals)がふづろいである(論文中の言い回しでは、時系列間隔が定数(constant)ではない)データであっても、このモデルはうまく対応できると論じられています。
それでは、論文に記述された数式表現を眺めることで、上に述べたことの具体的な状況を理解したいとおもいます。
従来のニューラル・ネットワークモデルとの違い
隣り合う2つの中間層の間で、順方向にデータを受け渡す演算式:従来のニューラル・ネットワークモデルの場合
従来の(多層)ニューラル・ネットワークモデルでは、隣りあう2つの中間層の間に起きていることは、以下の数式で表現されていました。
以下の数式(1)は、前の層(のあるノード ht)から次の層(のあるノードht+1)へとデータが受け渡される際に、データの値がどのような変換処理を受けるかを記述した数式です。
これまで述べてきたように、前の層(のあるノード ht)は、次の層(のあるノードht+1)と離散的に隔てられているため、2つの隣り合う層を表現する項は、htとht+1といったように、その下付き添字が、「1」という数値を挟んで、飛び飛びに並んでいます。(tとt+1の間の距離は1)
htとht+1の間には、ht+0.2もht+0.7524も存在しないのです。このように、それぞれの中間層(のなかにある各ノード)の並び方は、至るところ非連続であり、微分不可能なデータ系列です。
隣り合う2つの中間層の間で、順方向にデータを受け渡す演算式:提案モデルの場合
それに対して、提案モデルでは、モデル内の中間表現データ(個々のノードに相当するデータ表現値)は、至るところ微分可能な連続な”つながった”データ構造(をしているよう)です。
そのため、任意の2点間のデータで成立しているデータ値の変換式(2点間の数値の変化率)は、以下のような連続関数の微分演算で表現することができます。
損失関数の勾配学習則:連続関数の微分方程式演算
このように、データの中間表現が、至るところ微分可能な連続系列として表現される提案モデルでは、設定された損失関数(Loss function: L)は、従来の(多層)ニューラル・ネットワークで一般的に用いられる誤差逆伝播法(BP法:Back Propagation)ではなく、以下の数式(4)と数式(5)で表現されるようです。
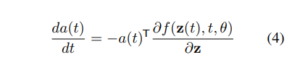
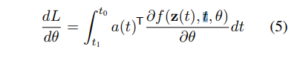
なお、損失関数は以下の数式(3)のように記述されます。
このあたりは、論文の第2節で、次の文章で説明されています。なお、以下の引用文中に出てくるODEとは、常微分方程式(Ordinary Differential Equation)のことで、ODE solverとは、常微分方程式の解を求めるアルゴリズムのことです。
そして、誤差逆伝播法に代わるreverse-mode differentiationの部分は、1962年にPontryaginほかによって提案された adjoint methodという数学演算技法が使われているようです。
論文の参考論文リストの中で、Lev Semenovich Pontryagin, EF Mishchenko, VG Boltyanskii, and RV Gamkrelidze. The mathematical theory of optimal processes. 1962. として、その論文名が掲載されています。
The main technical difficulty in training continuous-depth networks is performing reverse-mode differentiation (also known as backpropagation) through the ODE solver.
Differentiating through the operations of the forward pass is straightforward, but incurs a high memory cost and introduces additional numerical error. We treat the ODE solver as a black box, and compute gradients using the adjoint method (Pontryagin et al., 1962).
We present a modern proof of this method in Appendix B.
This approach computes gradients by solving a second, augmented ODE backwards in time, and is applicable to all ODE solvers. This approach scales linearly with problem size, has low memory cost, and explicitly controls numerical error.
そして、モデルの学習の流れの全体は、次の手順をたどるものとされています。

このあたりについて、僕はまだまだ理解が届いていませんので、今後、さらに勉強していこうと思います。
提案手法の概念実証テスト:教師あり学習など、3つのタスク・モデルを提案手法に置き換えて精度検証を実施
- 教師あり学習
- Continuous Normalizing flow
- Generative latent model
論文では、上記の3つの既存のモデルを、提案モデルに置き換えて、モデル学習を行い、既存モデルとの精度比較を行った結果を掲載しています。
提案手法はまだ概念提案段階:Wired誌でのインタビューより
なお、この論文を取材したWired誌によるインタビューに対して、論文の執筆者の1人は、この提案手法は、まだ概念提案段階にあると答えているようです。
同誌の和文訳出版の記事の結びの部分を、以下に引用します。
現時点では、デュベノー博士らの論文は、この新たな設計の概念実証を提供しているが、「広く使用されるようになるのはまだ先のことです」と博士らは述べる。AI分野で提案されてきた他の初期的な手法と同様に、実用化に至るには、具体化され、実験を通して改善されていく必要がある。とはいえ、この新たな手法は、イアン・グッドフェロー博士が発表した競争式生成ネットワーク(GANs)の論文に匹敵するような変革を、機械学習の分野にもたらす可能性がある。
「機械学習分野における主要な進歩の多くはこれまで、ニューラル・ネットワークの領域でもたらされました」とベクター研究所のリチャード・ゼメル研究所長は話す(氏は今回の論文には関与していない)。「デュベノー博士らの論文に追従するさまざまな研究がなされることになりそうです。とりわけ、医療分野などへのAI技術応用の基礎となる時系列モデルの分野においては顕著でしょう」。
いつの日かODEソルバーが爆発的に広まった暁には、最初にここで読んだことを思い出してもらえれば幸いだ。
この論文の執筆陣による後続の論文や、この論文に刺激を受けた他の研究者たちが、この「概念提案」をさらに豊かに発展させた後追い論文を公開されることを、期待したいと思います。


























